Matrix inversion

Inverse matrix A^-1 is defined as solution B to AB = BA = I. Traditional inverse is defined only for square NxN matrices, and some square matrices (called degenerate or singular) have no inverse at all. Furthermore, there exist so called ill-conditioned matrices which are invertible, but their inverse is hard to calculate numerically with sufficient precision.

ALGLIB package has routines for inversion of several different matrix types, including inversion of real and complex matrices, general and symmetric positive definite ones. ALGLIB can also invert matrices given by their triangular factorizations: LU or Cholesky decompositions. All versions of ALGLIB (C++, C# or other versions) provide same set of matrix inversion functions.

Matrix inversion algorithms

Triangular matrix inversion

Triangular matrices, like upper triangular U and upper unitriangular U₁ given below (and, of course, their lower triangular counterparts L and L₁), can be quite efficiently inverted in O(N³) time. Furthermore, because inverse of triangular matrix is also triangular, it is possible to perform in-place inversion - without ever allocating place for temporary copy of U/L.

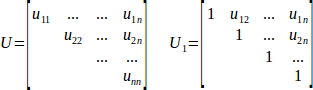
You can use following functions of matinv subpackage in order to invert triangular matrices:

• rmatrixtrinverse to invert real upper/lower triangular matrices (with support for unitriangular matrices)
• cmatrixtrinverse to invert complex upper/lower triangular matrices (with support for unitriangular matrices)

In all cases inversion result overwrites original matrix. Another triangle of the input matrix is left unchanged. And if you tell ALGLIB that matrix is unitriangular (i.e. has unit diagonal), then diagonal elements of the input matrix will be ignored too.

General matrix inversion (LU-based inversion)

Triangular matrix inversion function considered above can serve as basis for more general matrix inversion algorithms. Any general real/complex matrix A can be factorized as A=P·L·U, where P is a permutation matrix (used to improve numerical stability of the entire algorithm), L is a lower triangular one, and U is an upper triangular matrix (traditionally either L or U is normalized to have unit diagonal; ALGLIB convention is to normalize L). Such representation is called LU decomposition.

Thus, any general matrix can be inverted with three-step process: 1) calculate its LU factorization, 2) solve a sequence of triangular inversion problems to calculate general (non-triangular) inverse matrix, 3) account for permutation matrix P.

You can use following functions of matinv subpackage to invert general matrices:

• rmatrixinverse to invert real matrix
• cmatrixinverse to invert complex matrix

Functions mentioned above internally calculate LU decomposition of the input matrix A. If you already have this decomposition at hand, you can save significant amount of time by reusing it. Following ALGLIB functions can use already calculated LU decomposition:

• rmatrixluinverse to invert real matrix given by its LU factorization
• cmatrixluinverse to invert complex matrix given by its LU factorization

In all cases inverse matrix overwrites original input. All subroutines check condition number before inversion begins. If matrix is degenerate (one of triangular factors have zero element on its diagonal) or ill-conditioned (condition number is so high that there is a risk of overflow during inversion) then subroutine returns -3 error code and zero matrix.

Positive definite matrix inversion (Cholesky-based inversion)

Symmetric positive definite (for complex case: Hermitian positive definite) matrix can be inverted with same general-purpose LU-based algorithm, of course. However, for such matrices there exists better alternative - Cholesky factorization, which is representation of SPD matrix A as A = L·L^T, with lower triangular L (or, which is exactly same, A = U^T·U), with upper triangular U).

Cholesky-based matrix inversion has several benefits over LU-based one. First, instead of two factors (L and U) we now have only one triangular factor to invert. Less factors = less work. Second, there is no more row permutation matrix P. Row permutations are essential for the stability of LU decomposition, but Cholesky factorization is perfectly stable even without them (as long as your matrix is strictly positive definite). These permutations add significant overhead to algorithm running time because of two reasons: a) they trash CPU cache with non-local memory accesses, and b) they worsen parallelism potential by adding one more synchronization point to the algorithm.

You can use following functions of matinv subpackage to invert SPD/HPD matrices:

• spdmatrixinverse to invert real symmetric positive definite matrix
• hpdmatrixinverse to invert complex Hermitian positive definite matrix

Functions mentioned above internally calculate Cholesky decomposition of the input matrix A. If you already have this decomposition at hand, you can save significant amount of time by reusing it. In such cases call:

• spdmatrixcholeskyinverse to invert SPD matrix given by its real Cholesky factorization
• hpdmatrixcholeskyinverse to invert HPD matrix given by its complex Cholesky factorization

In all cases inverse matrix overwrites original input. All subroutines check condition number before inversion begins. If matrix is degenerate (one of triangular factors have zero element on its diagonal) or ill-conditioned (condition number is so high that there is a risk of overflow during inversion) then subroutine returns -3 error code and zero matrix.

Examples

ALGLIB Reference Manual has several examples of matrix inversion (in all programming languages supported by the library):

• matinv_d_r1 - an example of real matrix inversion
• matinv_d_spd1 - an example of real symmetric positive definite matrix inversion
• matinv_d_c1 - an example of complex matrix inversion
• matinv_d_hpd1 - an example of Hermitian symmetric positive definite matrix inversion

Benchmarks

Comparison with other free C# libraries

In this section we compare performance of the following free C# libraries:

• ALGLIB 3.12.0 for C# (Free edition) - pure C# version of our product
• Math.NET Numerics 3.20.0 (C# backend) - well known free numerical library, compiled with C# implementation of linear algebra backend
• Accord 3.8.0 - another free numerical library written completely in C#

Both Math.NET and ALGLIB for C# can utilize SIMD-capable linear algebra kernels (say, Intel MKL as backend), for in this benchmark we evaluate performance of 100% NET implementations. First, it is interesting to know how fast is C#. Second, in some cases you have to use 100% managed implementation. So, performance of NET implementation is important factor.

Our first comparison involves single-threaded inversion of 1024x1024 real matrix. This test was performed on 2.3GHz x64 Intel CPU, running Windows operating system. ALGLIB was compiled with Microsoft C# compiler, for other products we used precompiled NET 4.5 assemblies.

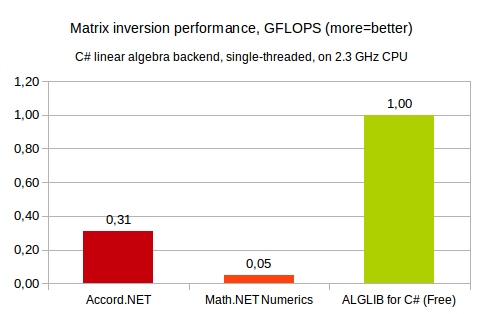
You may see that ALGLIB shows best results (in our experience - best results possible with pure C# implementation). Accord.NET is 3x times slower, and (very strange result) Math.NET is ~20x (!) times slower than ALGLIB. We believe that such low performance of Math.NET Numerics implementation is somehow connected with large matrix size. Their code seems to be optimized for small-scale problems.

Comparing C#, C++ and SIMD implementations

ALGLIB has several different implementations of linear algebra functionality, all with 100% identical APIs:

• 100% managed C# implementation - used by ALGLIB for C#
• generic C/C++ implementation - which can be used on platforms without high-performance SIMD-capable kernels (say, embedded systems)
• HPC implementation - highly optimized version of the library which can be used from C++ and C#, with assembly code for performance-intensive parts (including vendor implementations like Intel MKL)

Obviously, latter implementation is expected to be the fastest one :) But still, it is very interesting to compare performance of different programming environments (NET, generic C, SIMD-capable C). Our first comparison involves single-threaded inversion of 2048x2048 real matrix. This test was performed on 2.3GHz x64 Intel CPU, running Windows operating system.

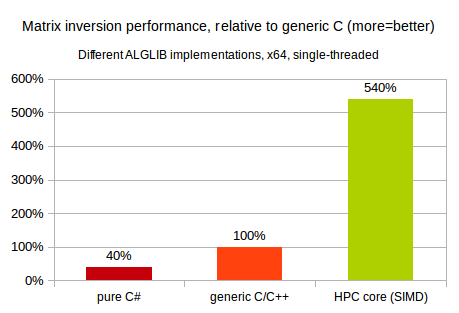
You may see that on x64 platform performance of pure C# code is ~2x times lower than that of generic C/C++ code. Our C# implementation of matrix inversion is optimized as much as possible, but still it is slower than generic C code. And, in turn, SIMD-capable code utilizing Intel MKL is many times faster than its generic C counterpart.

Additional notes

Avoiding explicit calculation of the inverse matrix

In many cases it is possible to avoid explicit calculation of the inverse matrix. Say, if you want to solve linear equation A·x=b, you can do so by calculating inverse matrix A^-1 and by performing matrix-vector multiplication. But far better approach is to use functions of densesolver subpackage which can solve linear system without forming A^-1 explicitly. You still have to perform LU/Cholesky decomposition, but at least you can skip matrix inversion phase. Another option is to use TRSV/TRSM (triangular solve-vector/solve-matrix) functions of ablas subpackage.

The general rule is that if you do not need coefficients of A^-1, but merely its product with some matrix/vector, there usually exists better way that explicit calculation of A^-1.

A few notes on CPU caches and performance

Naive implementation of the matrix inversion algorithm involves three nested loops, with inner one sequentially accessing all elements in the row/column. Such basic implementation, however, has major efficiency problems with matrices larger than 64x64 due to CPU cache issues. Algorithm performance can be as low as 10% of overall CPU potential, with most of the time being spent in cache misses.

The better solution is to use block-matrix approach, which splits large matrix into smaller blocks:

Such decomposition of larger problem into several smaller ones can be performed repeatedly several times, until operands fit into L1 cache of your CPU. If you perform decomposition in the recursive manner, with both operands having similar size, it is called "cache-oblivious approach". And if you prefer to factorize out small 32x32 (or similarly sized) chunk at the beginning/end of the problem, it is called "block-matrix approach". ALGLIB combines both approaches to deliver you best performance possible.

This article is licensed for personal use only.