
Cholesky decomposition of symmetric (Hermitian) positive definite matrix A is its factorization as product of lower triangular matrix and its conjugate transpose: A = L·LH. Alternative formulation is A = UH·U, which is exactly the same.
ALGLIB package has routines for Cholesky decomposition of dense real, dense complex and sparse real matrices. All versions of ALGLIB (C++, C# or other versions) provide same set of decomposition functions with similar interface.
1 Cholesky decomposition functions
General overview
Storage format
Dense Cholesky functions
Sparse Cholesky functionality
2 Benchmarks
Comparison with other free C# libraries
Comparing C#, C++ and SIMD implementations
3 Downloads section
Cholesky decomposition is quite similar to LU decomposition - it represents input matrix as product of two triangular matrices. Thus, it belongs to the family of so called triangular factorizations. However, it has several nice properties which LU does not.
First, Cholesky decomposition calculates just one triangular factor L instead of two (L and U). Less factors = less work, and indeed, operation count for Cholesky is roughly two times smaller than that of LU decomposition (N3/3 FLOPs vs 2·N3/3 FLOPs).
Second, Cholesky decomposition is stable even without pivoting (row/column permutation which moves largest element to the diagonal). This pivoting stage involves only a few operations, but with bad cache locality - so dropping pivoting results in better performance.
Finally, Cholesky decomposition can be easily (in O(N2) time) updated: there exists cheap algorithm for calculation of rank-1 update {{Au = A + u'·u.
Symmetric matrices are traditionally represented by their upper or lower triangle (just one of them, at your choice).
And Cholesky factor L (or U) occupies exactly one triangle too.
So it is very convenient to have half of your symmetric matrix on input replaced by Cholesky factor on output.
Thus, all Cholesky factorization routines in ALGLIB accept additional parameter isupper,
which tells ALGLIB what part of the input matrix contains data.
On output this part of the matrix is replaced by L (when lower triangle is used) or U (when upper one is used to store matrix),
and another triangle is not changed (not referenced at all during computations).
Dense Cholesky decomposition can be calculated with following functions of trfac subpackage:
One more interesting function is spdmatrixcholeskyupdateadd1, which updates Cholesky decomposition of rank-1 updated matrix Au = A + u'·u.
Sparse matrices often arise in large-scale linear algebra and optimization problems. ALGLIB supports several types of sparse storage formats (CRS, Skyline/SKS and flexible hash-table based representation), rich set of BLAS-like functions and has some limited support for sparse matrix factorization.
If your sparse matrix has limited profile (i.e. it can be efficiently stored in Skyline/SKS format), you can factorize it with sparsecholeskyskyline (trfac subpackage again).
In this section we compare performance of the following free C# libraries:
We should point out that both ALGLIB for C# and Math.NET Numerics can utilize high-performance native linear algebra kernels (like Intel MKL), but for the purposes of this benchmark we evaluate performance of pure C# implementations. First, it is interesting to know how much performance pure NET can bring us. Second, in some cases you are literally forced to use 100% managed implementation without even a bit of unsafe code. So, performance of NET implementation is important factor. Anyway, subsequent sections will compare pure NET vs native kernels.
Our first comparison involves single-threaded Cholesky decomposition of 2048x2048 symmetric positive definite matrix. This test was performed on 2.3GHz x64 Intel CPU, running Windows operating system. ALGLIB was compiled with Microsoft C# compiler. All other products were installed with NuGet (NET 4.5 assemblies were used).
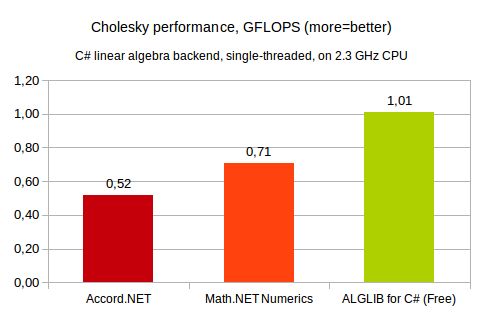
You may see that ALGLIB does its best - it is 2x faster than Accord.NET, and roughly 40% faster than its closest competitor, Math.NET. Such difference in performance is explained by better algorithmic optimizations applied to the library. However, absolute results are not very impressive - way below that of generic C code (see next section), not to mention SIMD-capable implementations. Well, C# is not high-performance language, after all.
ALGLIB provides several different implementations of linear algebra functionality, all with 100% identical APIs:
Obviously, first implementation (pure C#) is the slowest one, whilst HPC implementation is the fastest. But what about exact numbers? Our first comparison involves single-threaded Cholesky decomposition of 2048x2048 symmetric positive definite matrix. This test was performed on 2.3GHz x64 Intel CPU, running Windows operating system.
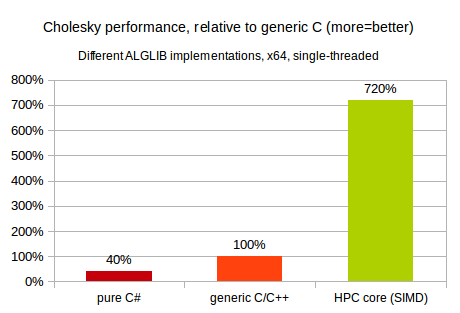
You may see that on x64 platform performance of pure C# code is many times lower than that of generic C/C++ code. We optimized C# implementation of Cholesky decomposition as much as possible, but still it is roughly 2.5x times slower than C/C++ code (even without SIMD!). And, in turn, generic C/C++ code is many times slower than SIMD-capable code utilizing Intel MKL.
This article is licensed for personal use only.
ALGLIB Project offers you two editions of ALGLIB:
ALGLIB Free Edition:
+delivered for free
+offers full set of numerical functionality
+extensive algorithmic optimizations
-no multithreading
-non-commercial license
ALGLIB Commercial Edition:
+flexible pricing
+offers full set of numerical functionality
+extensive algorithmic optimizations
+high performance (SMP, SIMD)
+commercial license with support plan
Links to download sections for Free and Commercial editions can be found below:




