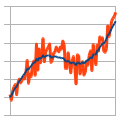
Moving average filters

Moving average filter (also known as rolling average, running average) is a time series filter which calculates running weighted sum of time series.

ALGLIB package provides you with dual licensed (open source and commercial) implementation of SMA/LRMA/EMA filters in several programming languages, including our flagship products:

• ALGLIB for C++, a high performance C++ library with great portability across hardware and software platforms
• ALGLIB for C#, a highly optimized C# library with two alternative backends: a pure C# implementation (100% managed code) and a high-performance native implementation (Windows, Linux) with same C# interface

Moving average filters

SMA (simple moving average)

Simple moving average filter, denoted as SMA(k), is a finite impulse response filter. For any moment t it returns average of previous k values (or t values, for t<k). This filter has nice property that for any filter width k and time series length N its output can be efficiently calculated in O(N) time (no dependence on k).

SMA(k) filter is implemented in ALGLIB by the filtersma function. An example of usage can be found in ALGLIB Reference manual: filters_d_sma.

Note #1
One major distinction is that between centered and uncentered versions of the filter. Former uses both past and future values of time series, i.e. FILTER(time=t) = AVG(..., x_t-1, x_t, x_t+1, ...). Latter uses only past and present values to calculate filter output: FILTER(time=t) = AVG(..., x_t-2, x_t-1, x_t). As for now, ALGLIB implements only uncentered version of SMA(k) filter (only past/present values are used). If you need centered version, you may obtain it by simply shifting filter output by (k-1)/2 forward in future (for odd filter width k).

EMA (exponential moving average)

Exponential moving average filter, denoted as EMA(k), is an infinite impulse response filter, a transformation of time series according to the formula below:

EMA(k) filter is implemented in ALGLIB by the filterlema function. An example of usage can be found in ALGLIB Reference manual: filters_d_ema.

LRMA (linear regression moving average)

Linear regression moving average filter, denoted as LRMA(k), is a finite impulse response filter, which fits straight line to a sliding window with width k. Although LRMA filtering costs more than simple or exponential moving average filters (its running time is O(N·k)), linear regression moving average estimate tends to better follow the trend line.

LRMA(k) filter is implemented in ALGLIB by the filterlrma function. An example of usage can be found in ALGLIB Reference manual: filters_d_lrma.

This article is licensed for personal use only.