Elliptic integrals of the first and second kind

Elliptic integrals originally arose from the problem of elliptical arc length calculation. Now, elliptic integral is any function having the following form:

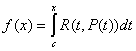
where R(x,y) is a rational bivariate function, P(t) is the square root of a polynomial of degree 3 or 4 with distinct roots, and c is a constant. In general, elliptic integrals cannot be expressed in terms of elementary functions. However, with the appropriate reduction formula, every elliptic integral can be brought into a form that involves integrals over rational functions and the three canonical forms (i.e. the elliptic integrals of the first, second and third kind). This module contains subroutines that calculate elliptic integrals of the first and second kind).

Elliptic integrals of the first kind

Incomplete elliptic integral of the first kind has the following form:

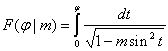
It is calculated by using the IncompleteEllipticIntegralK subroutine.

The important special case of incomplete elliptic integral is the complete elliptic integral of the first kind:

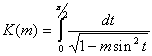
It is calculated by using the EllipticIntegralK subroutine.

It should be noted that there is a singularity in m=1. In the neighborhood of this point (neighborhood diameter is comparable to machine precision) the calculation accuracy decreases. At the same time, in the neighborhood of 0, numbers are represented with high precision. Therefore, if we need high precision in the neighborhood of singularity, we can use the EllipticIntegralKHighPrecision subroutine which calculates not K(m), but K(1-m). This moves singularity in the point m=0.

Elliptic integrals of the second kind

Incomplete elliptic integral of the second kind has the following form:

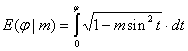
It is calculated by using the IncompleteEllipticIntegralE subroutine.

The important special case of incomplete elliptic integral is the complete elliptic integral of the second kind:

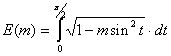
It is calculated by using the EllipticIntegralE subroutine.

This article is licensed for personal use only.