
QR decomposition is a best known decomposition from a whole family of orthogonal factorizations, which includes QR, LQ, RQ and QL decompositions. Here Q denotes orthogonal matrix, R and L denote upper and lower triangular matrices. These decompositions may be used to solve full rank least squares problem, as preliminary step in the construction of the SVD decomposition, or for other tasks.
ALGLIB package has C/C++ and C# implementations of two most popular decompositions: QR and LQ. QL and RQ decompositions are less popular and they are not implemented in the ALGLIB.
1 Aglorithm
2 QR decomposition functions
Storage format
ALGLIB functions
3 Benchmarks
Comparison with other free C# libraries
Comparing C#, C++ and SIMD implementations
4 Downloads section
The most traditional approach to QR decomposition is to represent orthogonal Q as a sequence of Householder reflections. Coefficients of these reflections can be stored in-place, replacing lower triangular entries of input matrix (ones unoccupied by upper triangular R). Well, almost inplace - we need N additional elements denoted Tau. Thus, typical QR decomposition subroutine on input takes square/rectangular matrix A and on output it:
QR decomposition functionality is located in ortfac (orthogonal factorizations) subpackage. Following functions can be used with real matrices:
Exactly same set of functions is provided for complex matrices:
In this section we compare performance of the following free C# libraries:
Although both ALGLIB for C# and Math.NET have high-performance native linear algebra kernels, for the purposes of this benchmark we evaluate performance of pure C# implementations. First, it is interesting to know how much performance NET can bring us. Second, in some cases you have to use 100% managed implementation.
Our first comparison involves single-threaded QR decomposition of 1024x1024 general real matrix. This test was performed on 2.3GHz x64 Intel CPU, running Windows operating system. ALGLIB was compiled with Microsoft C# compiler, for other products we used precompiled NET 4.5 assemblies.
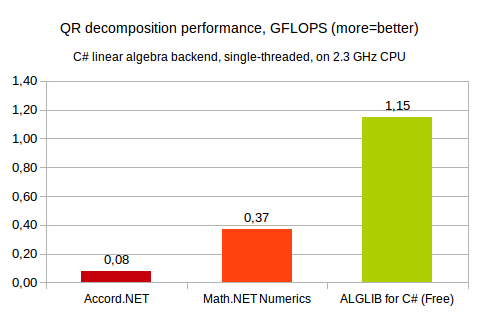
You may see that ALGLIB shows best results close to performance limits of C# language. Accord.NET is ~14x slower, whilst Math.NET is "just" ~3x slower than ALGLIB.
Another interesting topic to consider is relative performance of C#, generic C/C++ and SIMD-capable implementations. ALGLIB provides several different implementations of linear algebra functionality, all with 100% identical APIs:
You may guess that these implementations are sorted by performance, with latter being fastest one :) But how fast is it? Our comparison involves single-threaded QR decomposition of 2048x2048 matrix. This test was performed on 2.3GHz x64 Intel CPU, running Windows operating system. Generic C/C++ version is used as baseline one.
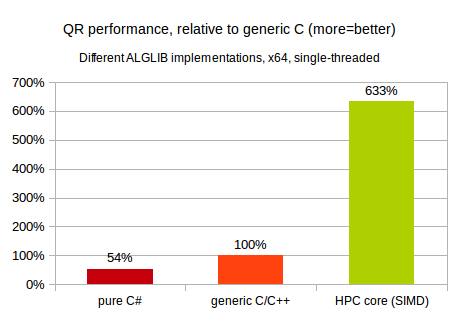
You may see that on x64 platform performance of pure C# code is roughly two times lower than that of generic C/C++ code. And, in turn, generic C/C++ code is many times slower than SIMD-capable code utilizing Intel MKL.
This article is licensed for personal use only.
ALGLIB Project offers you two editions of ALGLIB:
ALGLIB Free Edition:
+delivered for free
+offers full set of numerical functionality
+extensive algorithmic optimizations
-no multithreading
-non-commercial license
ALGLIB Commercial Edition:
+flexible pricing
+offers full set of numerical functionality
+extensive algorithmic optimizations
+high performance (SMP, SIMD)
+commercial license with support plan
Links to download sections for Free and Commercial editions can be found below:




