Neural networks: improving generalization

In this article we'll review basic concepts of machine learning, like space of models, noise, early stopping, regularization. We'll consider solution of the noisy problem with ALGLIB neural network functions, but won't dive into the technical details (what functions to call or what network architectures to use). If you want to know more about ALGLIB Neural Networks, you can read other articles in this section.

Problem statement

Consider following problem - we have to determine probability of breaking smartphone when dropping it from X meters. As solution we need neural network which accepts the only parameter - height, and returns probability of smartphone failure.

We know for sure that our smartphone will survive when dropped from 0.2 meters or lower, and will be broken when dropped from 1.2 meters or higher. So we just take 110 phones, divide them into 11 groups (10 phones in each), and - drop them from different heights, from 0.2 to 1.2 meters with step equal to 0.1. As result, we get a lot of broken phones - and statistics, which allow us to build empirical chart (below, left). Assume that somehow we know "ideal" curve (below, right).

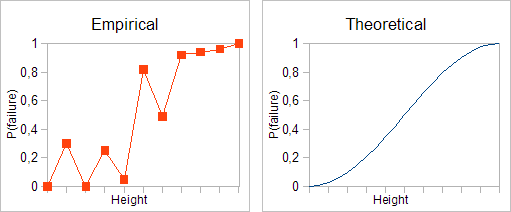
In theory, we have everything we need to determine failure probability. We have experimental data. We can interpolate between them to determine values at intermediate points. We do not even need neural network! The problem is that empirical chart is non-monotonic. It is obvious that larger height means larger probability of failure, but our data do not respect this rule. The reason is noise in data.

In data analysis, noise is a deviation of experimental data from "ideal" values predicted by theory. Noise can have many sources. In our case the reason is finite size of sample, which was used to measure empirical probabilities. We've used only 10 measurements to calculate each probability - it is no wonder that we have such large fluctuations. But what can we do with noise?

First of all, it is not needed and even harmful to exactly reproduce noise. From two curves - red and blue - we need latter one. We can easily reproduce red curve by neural network with 100 neurons in 2 hidden layers - flexible and trainable. But such solution is called "overfitted" - full fit to experimental data, but only vague resemblance of true probabilities. Conclusion: if overfitted network is bad, we need some other, not-overfitted network.

Below we consider three approaches to solution of the overfitting issue.

Preventing overfitting

Early stopping

Neural network - it is geometry + weight coefficients. Training is a movement through space of coefficients from initial state (usually random) to the final state (minimum of some fitness function). We can consider space of coefficients as space of models, with every point corresponding to some neural network. Neural networks can have tens or thousands of coefficients, but your browser can't render even 5-dimensional pictures, so we will limit our article by 2D images.

Chart below visualizes typical training process. Network geometry is not important for this article; you can assume that it has one hidden layer with 20 neurons. In this case training is just a minimization of overall deviation from experimental data/ We start from the point at the bottom right corner - random set of weights. Red line is a network output at [0.2,1.2], gray line represents "ideal" values. You can see that random fluctuations of network output are very far from desired values. So training algorithm starts to fit network output to our data. Process is performed step by step, until we stop at the final point (top, right), where experimental data are reproduced almost exactly (within accepted tolerances).

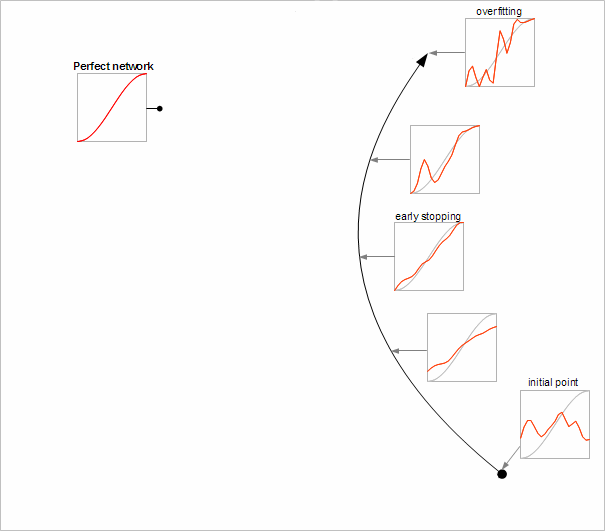
Training process almost always have three stages, which are same for any network:

1. At the first stage, when we depart from the initial point, neural network starts to slowly change its outputs, but they are still far from the training set. This stage corresponds to the first point, which is marked as "initial point".
2. At the second stage neural networks learns to reproduce general trends in data, but it does not reproduce minor features of the dataset. This stage corresponds to the second, third and fourth intermediate points.
3. At the last stage neural network learns to reproduce dataset exactly, with all details and noise. This is the last point at our chart, which corresponds to the exact minimum of the training error.

You may notice that we have one more point at our chart - perfect network. However, this perfect network is outside of our path through the model space. The truth is that perfect neural network is possible - but almost always we don't have enough data to find it.

First overfitting prevention technique consists in artificial termination of the training process. Hence its name - early stopping. For example, we may stop at the third point, where neural network sufficiently close reproduces ideal curve. The question is how to determine stopping point. Traditionally, 3-way splitting of the dataset is used - it is split into training, validation and test sets. Training algorithm minimizes error on the training set, and terminates process when validation error starts to grow. Generalization error is estimated using test set. You can study this technique in more details in other sources (Wikipedia, faqs.org).

Note #1
Alternative solution exists - studying of the network by human expert, which decides whether to continue training or to stop it. However, this approach is hard to formalize and can be useful only for low-dimensional problems with known result.

The main drawback of this approach is that it requires a lot of data, because only part of the dataset is used for training. In our case (11 points) it is very hard to divide dataset into three subsets and still have enough data for training. This drawback makes early stopping less popular than weight decay (regularization), which is considered in the next section.

Weight decay (regularization)

The second approach is to modify target function which minimized during training. Overfitted neural network reproduces the finest details of noise in the dataset. Noise is non-smooth by its nature - thus, neural network tries to reproduce non-smooth function. Neural network must have very large coefficients in order to reproduce non-smooth function - many times larger than ones which are required to reproduce noise-free smooth function. When coefficients are small, neural network has smooth outputs which change slowly.

If you look at training process in more details, you will see that until some moment (end of the second stage) average magnitude of the coefficients is moderate. But as soon as network starts to overfit, coefficients sharply increase in magnitude. There exists strong dependence: large coefficients = overfitting. It means that we can prevent network from overfitting by limiting growth of its coefficients.

In order to achieve this we minimize more complex merit function: f=E+λS. Here E is a training set error, S is a sum of squares of network weights, and decay coefficient λ controls amount of smoothing applied to the network. Optimization is performed from the initial point and until the successful stopping of the optimizer. In the previous case (early stopping) we terminated optimization in the middle of process, but now we optimize until the end.

Chart below shows us a spectrum of neural networks trained with different values of λ – from zero value (no regularization) to infinitely large λ. You may see that we control tendency to overfit by continuously changing λ. Zero λ corresponds to overfitted network. Infinitely large λ gives us underfitted network, equal to some constant. Between these extremal values there is a range of networks which reproduce dataset with different degrees of precision and smoothness. Again, you may see that perfect network is outside of this range.

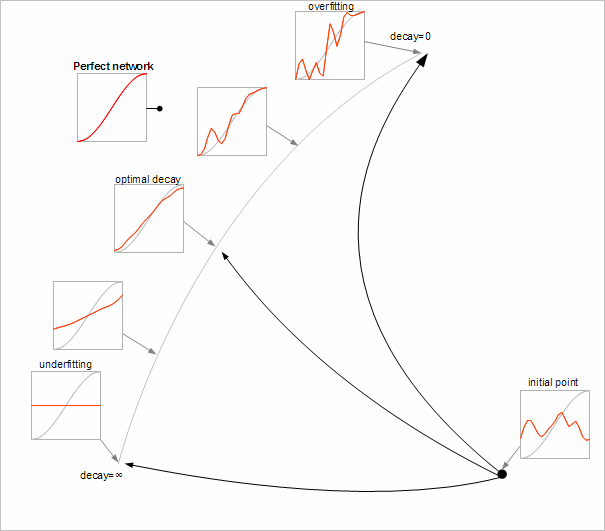
We can choose good neural network by tuning λ - weight decay coefficient. Optimal lambda can be selected by using test set or cross-validation (in this case all dataset can be used for training).

Note #2
We may note that we've explained regularization in terms of limit on the growth of network coefficients. Such approach is intuitive, but from theoretical point of view it is not 100% correct. More correct explanation of regularization involves Bayesian formalism or VC dimensionality.

Models with reduced complexity

Third approach is to use neural network with reduced complexity. Network contains as little neurons as possible. If we are lucky, it will be so flexible that it will be able to train - but not enough flexible to overfit. Such approach has benefits (in particular - high performance), but it has many important drawbacks. Very often it is impossible to have moderately flexible network - either it is way too rigid, or it is too flexible. Another source of problems is sharp change in the network complexity (and generalization error) after addition/removal of neuron - control over generalization/overfitting is non-smooth.

Comparison of different approaches

Main idea of early stopping can be explained as: "move to bad solution, but stop halfway". Main idea of regularization can be explained as: "move to good solution". Main idea of third approach can be explained as: "only good solutions are possible".

From our point of view, regularization is preferred option. It is more flexible, it allows to continuously change model complexity, it uses entire dataset for training. In some cases early stopping is possible and even preferable, this method is used by early stopping ensembles. However, when you solve new problem we recommend you to start from regularization (weight decay) and resort to other methods only after failure of regularization.

One more solution of the overfitting issue is to choose another neural model - instead of individual network you can use ensemble of networks. Ensembles of networks are less prone to overfitting than individual networks.

This article is licensed for personal use only.