Bicubic interpolation/fitting

Bicubic spline is a fast and precise two-dimensional interpolation and fitting method. ALGLIB package contains an implementation of 2D splines available in several programming languages:

• ALGLIB for C++, a high performance C++ library with great portability across hardware and software platforms
• ALGLIB for C#, a highly optimized C# library with two alternative backends: a pure C# implementation (100% managed code) and a high-performance native implementation (Windows, Linux) with same C# interface

Our implementation of 2D splines:

• supports bicubic and bilinear splines
• supports operations like interpolation, differentiation, linear transformation, serialization
• allows you to fit bicubic splines to large-scale datasets (with up to 100M points), which makes splines a competitive replacement for RBFs or thin plate splines on 2D problems

Getting started and examples

Getting started

Bicubic spline interpolation functionality is provided by the spline2d subpackage of ALGLIB package. A bicubic spline can be created from the data sampled at the regular grid (to be exact, more general rectilinear one) with spline2dbuildbicubicv function. This function supports both scalar and vector-valued splines.

After an instance of spline object is built, you can perform following operations:

• evaluate spline with spline2dcalc (for a scalar spline) or spline2dcalcv, spline2dcalcvbuf and spline2dcalcvi (for a vector-valued spline) functions
• evaluate spline derivative with spline2ddiff and spline2ddiffvi (for a vector-valued spline) functions
• perform linear transformation of the spline by means of spline2dlintransf and spline2dlintransxy functions
• serialize/unserialize it with spline2dserialize and spline2dunserialize functions

ALGLIB Reference Manual includes following examples which show how to work with bicubic splines:

• spline2d_bicubic - spline creation and basic operations
• spline2d_copytrans - linear transformation
• spline2d_unpack - unpacking spline coefficients
• spline2d_vector - working with vector-valued splines

Fitting splines to scattered data

In the previous section we mentioned that bicubic spline needs data to be sampled at the regular grid. The reason is that internally bicubic spline is composed of many rectangular cubic patches, so there must be a one-to-one correspondence between spline nodes and dataset points. Such one-to-one correspondence allows fast and memory-efficient construction of the bicubic spline from the array of spline values.

However, it is also possible to fit bicubic spline in the least squares sense to the irregular (scattered) data. Efficient utilization of the problem sparsity allows us to solve really large tasks - to utilize grids from 100x100 to 500x500 nodes or even (with FastDDM algorithm) with 10.000x10.000 nodes.

ALGLIB has two least squares solvers for bicubic splines:

• BlockLLS solver, which fits bicubic spline (single global model is fitted) to the irregularly sampled data with optional nonlinearity penalty being applied. This algorithm is the easiest to use and control in ALGLIB (only one parameter to control - penalty coefficient). From the other side, it is limited by roughly 500x500 grids (250K nodes) and has limited parallelization potential.
• FastDDM solver, which splits the dataset into smaller chunks and fits multilayered spline models which are "glued" together later. This algorithm is a bit harder to control than BlockLLS because you have to tune two parameters: the regularization coefficient and the number of layers. However, its strong sides are the ability to handle grids with up to 10000x10000 nodes and good parallelization properties.

An example of bicubic spline fitting - spline2d_fit_blocklls - can be found in ALGLIB Reference Manual.

Benchmarks

Medium-scale problems: bicubic spline fitting vs RBFs

Radial basis function interpolation is a well-known method of handling scattered multidimensional data. ALGLIB includes sophisticated implementation of RBFs called HRBF (Hierarchical RBF). Our implementation of RBFs uses many algorithmic improvements and is much faster than straightforward attempt to fit RBFs by solving huge dense linear systems. However, in the 2D case bicubic splines become a viable alternative with an order of magnitude improvement in both memory consumption and running time.

Our first test compares ALGLIB multilayered RBFs vs. BlockLLS and FastDDM bicubic solvers. We tested running times of these methods on a 96x96 grid being fitted to 20K randomly generated points. A hierarchical RBF model was configured to fit three successive layers with initial radius set to 1.0. Such problem can be classified as medium scale one (roughly 10.000 parameters to fit). A 4-core 3.5 GHz x64 CPU running C++ version of the ALGLIB (Intel MKL included) was used.

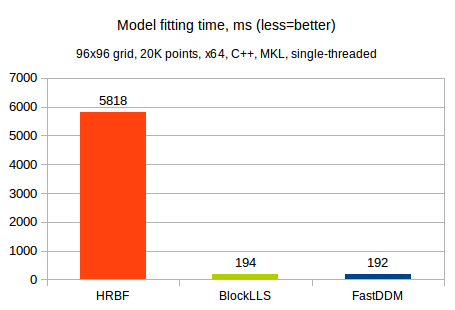
You can see that both bicubic fitting algorithms (BlockLLS and FastDDM) were much faster than HRBF.

Large-scale problems: BlockLLS vs FastDDM

The main difference between BlockLLS and FastDDM solvers is that former solves entire problem in one step and latter uses recursive divide-and-conquer approach.

The BlockLLS method uses sparse LSQR linear solver with block septa-diagonal preconditioner matrix (hence the method's name). The linear systems being solved are extremely sparse but nevertheless, for grids larger than 512x512 even highly optimized BlockLLS becomes too memory-hungry. The FastDDM algorithm solves this problem by splitting large tasks into smaller chunks and handling them with BlockLLS-like "basecase" algorithm.

We tested running times and memory consumption of both methods on a 512x512 grid being fitted to 525K randomly generated points. The same CPU as in the previous test was used. Below we compare running times of single threaded BlockLLS and FastDDM solvers:

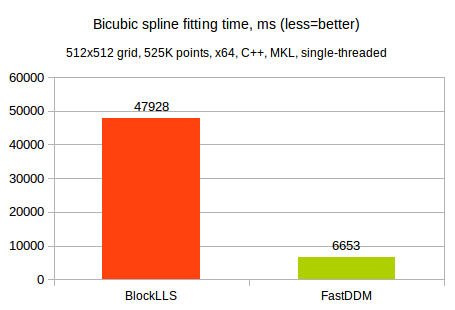
Well, we have to say that both solvers show impressive results. A 512x512 grid means that we have 262.000 variables to fit. Being able to solve such huge least squares problem in just 48 seconds (BlockLLS time) is impressive anyway. And 7 seconds spent by FastDDM are even more impressive.

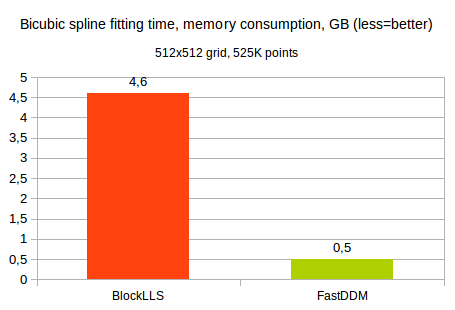
Just for comparison, a brute-force attempt to use dense Cholesky solver would need about 150.000-200.000 seconds (roughly 2 days!) and about 500 GB of memory. Contrary to that, BlockLLS needs roughly 4.6 GB of memory (actual memory consumption according to OS stats), and FastDDM needs just 0.5 GB:

This article is licensed for personal use only.