Singular spectrum analysis (SSA)

Singular spectrum analysis (SSA, also known as Caterpillar-SSA) is a non-parametric time series analysis method. It can be used to filter out noise components or to predict future values.

ALGLIB package includes highly optimized SSA implementation available in several programming languages, including:

• ALGLIB for C++, a high performance C++ library with great portability across hardware and software platforms
• ALGLIB for C#, a highly optimized C# library with two alternative backends: a pure C# implementation (100% managed code) and a high-performance native implementation (Windows, Linux) with same C# interface

Our implementation of singular spectrum analysis includes following features (see below for more detailed discussion):

• high-performance C++/C# code scalable to big data loads
• flexible and convenient interface, with an ability to analyze single/multiple time series and perform various kinds of analysis (noise suppression, noise/trend separation, prediction, basis extraction)
• specialized real-time analysis options: ability to quickly rebuild basis when just one/few values are added to the dataset

Getting started and examples

Getting started

Singular spectrum analysis is provided by the ssa subpackage of ALGLIB package. Everything starts with SSA model creation, which is performed by means of the ssacreate function. This function initializes an instance of the ssamodel class, which can be used to perform various kinds of activities.

We tried to make SSA models as easy as possible, so you can treat it as some kind of calculator. Just tell ALGLIB what data you have, and what kind of analysis you need: (1) create the model, (2) add the data to the model, (3) set analysis options, (4) perform an analysis.

Here analysis options are eigensolver being used, window width, components count and several other performance-related settings which are discussed below. And analysis can be basis extraction, trend/noise separation, forecasting (and extraction of linear recurrence relation coefficients).

Examples

We prepared several examples (in C++, C# and all other programming languages supported by ALGLIB) of SSA usage with ALGLIB:

• ssa_d_basic - the very simple example of trend/noise separation with SSA on toy dataset
• ssa_d_forecast - forecasting with SSA
• ssa_d_realtime - real-time analysis of constantly arriving data

Sections below discuss these examples in more details.

Singular spectrum analysis (SSA) in ALGLIB

Creating SSA model object

Singular spectrum analysis is provided by the ssa subpackage of ALGLIB package. An SSA model is created with ssacreate function. This function initializes an instance of the ssamodel class, which can be used to perform various kinds of activities.

Specifying dataset

SSA model works with single/multiple sequences of data. The most frequent case of time series analysis is a situation when you have "just one big sequence of values", i.e. all you data form single contiguous sequence. Such sequence can be specified with the ssaaddsequence function.

This function has "add" semantics, i.e. multiple calls to this function will result in multiple sequences being stored internally by the model object. Say, it is possible to store five sequences corresponding to five different periods (days/months/...). These sequences will be analyzed together to create a common basis, but solver will assume that they are independent, i.e. no overlap exists between different sequences.

Another situation is when you have a constant stream of arriving data and want to reuse results of the previous analysis as much as possible. Say, new values are appended to the dataset every second, and new basis constructed by SSA is almost same as one constructed one second earlier. In this case, you may use the ssaappendpointandupdate function, which adds one/several points to the end of the dataset and performs a quick update of the previously computed basis. There also exist similar function, ssaappendsequenceandupdate, which adds new independent sequence.

Selecting/configuring SSA algorithm

The most time-consuming part of SSA is an eigensolver which finds singular vectors. ALGLIB includes several singular spectrum analysis algorithms, which perform exactly same analysis, but use different approaches to compute singular vectors:

• A "real-time top-k" algorithm (recommended), activated by the ssasetalgotopkrealtime function, which uses subspace iteration approximate eigensolver with O(SeriesLength·WindowWidth²) initial running time and fast O(k·WindowWidth²) incremental updates.
• A "direct top-k" algorithm, activated by the ssasetalgotopkdirect function, which uses direct eigensolver with O(SeriesLength·WindowWidth²) initial running time and O(WindowWidth³) incremental updates.
• A "precomputed" algorithm, activated by the ssasetalgoprecomputed function, which uses user-supplied matrix of singular vectors.

Component count K is selected when you select an SSA algorithm. Another important option is analysis window width, which is chosen with ssasetwindow function.

Trend/noise separation

Most frequent use of singular spectrum analysis is to perform trend/noise separation. After you specified a dataset for analysis, an analysis algorithm, a window width and a components counts, you may perform analysis with one of the following functions: ssaanalyzesequence and ssaanalyzelast.

First one, ssaanalyzesequence, analyzes user-specified sequence (not necessarily one used for basis computation) and returns trend and noise components separated. Latter is a convenience wrapper which performs analysis of the last N ≥ WindowWidth values of the time series stored in the model.

Forecasting

SSA forecasting can be performed with one of the functions below:

• ssaforecastsequence, which forecasts NForecast future values of user-specified sequence (not necessarily one used for basis computation). Forecasting is performed using WindowWidth-1 last values of the sequence.
• using just one - last - window may result in noisy predictions, so here comes the next function: ssaforecastavgsequence. This function performs M independent predictions using M last windows and averages results.
• finally, ssaforecastlast and ssaforecastavglast functions are convenience versions of functions above, which operate on the last sequence stored in the model.

Other functions

You may want to extract some information internally stored in the model:

• you can extract basis computed by the current algorithm by means of the ssagetbasis function
• you can extract coefficients of linear recurrence relation used for prediction with the ssagetlrr function

Real-time and big-data features

Real-time SSA algorithm can perform really fast updates of previously computed basis when new data arrive. Explicitly tell ALGLIB that new values are appended to the end of the dataset by calling ssaappendpointandupdate or ssaappendsequenceandupdate function, and it will be able to perform quick O(k·WindowWidth²) basis update instead of performing O(SeriesLength·WindowWidth²) calculation from scratch. Such algorithm greatly accelerates some "long-running" use cases.

From the other side, incremental updates are fast, but the initial calculation of the basis still has O(SeriesLength·WindowWidth²) cost. Your program may perform well in the long run, but initial "power up" may be too slow. Thus, ALGLIB provides you with one more performance-related option: "delayed power-up", which is activated with the ssasetpoweruplength function. This function allows you to split costly initialization amongst T first iterations, with each of them having reduced O((SeriesLength/T)·WindowWidth²) cost.

As result, first T attempts to perform an analysis will return somewhat inaccurate basis (1/T-th of the entire dataset will be used for the first analysis run, 2/T-th - for the second portion of incoming data, and so on), but eventually algorithm will "warm up" and start to return precise results.

Benchmarks

Backends: C++ (native) vs C# (managed)

ALGLIB package has several versions in various programming languages, relying on two primary backends: (a) native computational core, and (b) 100% managed computational core (.NET framework). In addition, commercial edition of ALGLIB for C# can access native computational core (with exactly the same C# API being provided).

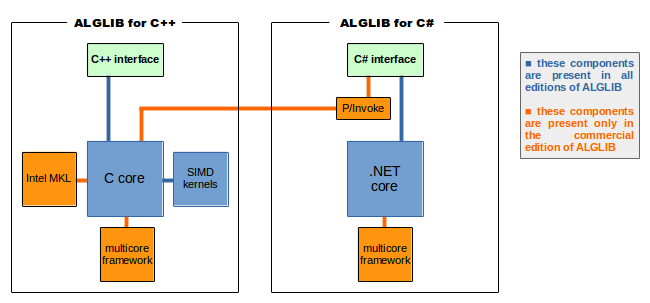
Thus, leaving aside multithreading, we have three primary options to study:

• 100% managed C# implementation - used by ALGLIB for C#
• open source C/C++ implementation - used by C++ version of ALGLIB
• HPC implementation - high-performance version of the library which can be used from C++ and C#

Obviously, first implementation (pure C#) is the slowest one, whilst HPC implementation is the fastest. But what about exact numbers? Our first comparison involves single-threaded SSA of 7200 ticks long signal, with window width set to 256, and 10 principal components being extracted. Real-time version of SSA algorithm is used. This test was performed on 2.3GHz x64 Intel CPU, running Windows operating system.

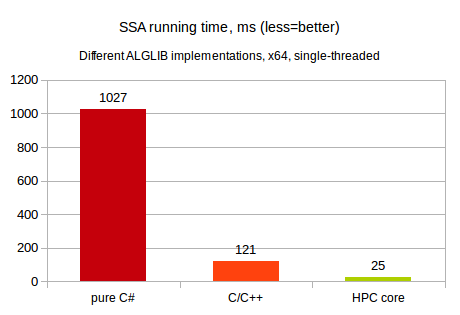
Conclusion: native linear algebra wins! :)

Algorithms: direct solver vs real-time one

Two most time-consuming phase of singular spectrum analysis is initial calculation of trajectory matrix product A=X'·X. Second, less costly phase, is eigenvalue decomposition of A. Furthermore, incremental updates to the model with ssaappendpointandupdate function add two more distinct phases: updating A and updating evd(A).

Different SSA solvers perform these phases in different manner:

• "Direct top-K" SSA algorithm performs straightforward calculation of A with Level 3 BLAS functions, and calculates complete EVD of A before truncating everything except for top K eigentriples. Incremental updates of A are calculated very efficiently, but evd(A) is recalculated from scratch every time.
• "Real-time top K" SSA calculates A using same BLAS functions, but evd(A) is calculated via subspace iteration eigensolver which quickly (albeit less precisely) finds just K required eigentriples. Because subspace eigensolver supports efficient "warm restarts", incremental updates are performed even more efficiently than with "direct" solver.
• Finally, "real-time SSA with power-up cycle" splits costly evaluation of A=X'·X between several subsequent incremental updates of SSA model.

On the chart below you may see running times for 4 subsequent basis calculations with ssagetbasis: initial basis calculation and three subsequent updates performed with same settings as ones used for our previous benchmark:

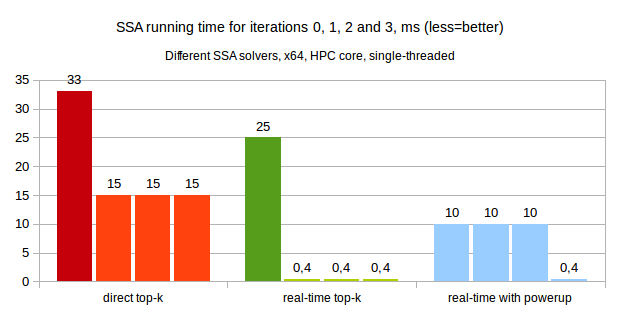
As you may see, "direct" solver has highest running times for both initial basis calculation and incremental updates. "Real-time" solver has comparable initial basis calculation time, but orders of magnitude faster incremental update. Finally, power-up feature allows us to spread computational load more evenly across iterations.

This article is licensed for personal use only.