Chebyshev polynomials

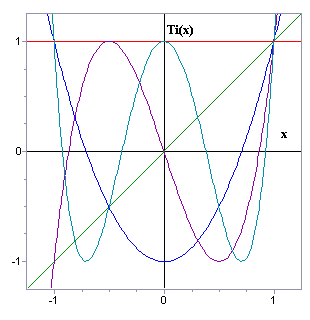
The Chebyshev polynomials of the first (T_n and second (U_n) kinds can be defined by the trigonometric identity

T_n(x) = cos(n arccos x)
U_n(x) = sin((n+1) arccos x) / sin( arccos x)

or can be constructed using the three term recurrence relation:

T₀(x) = 1
T₁(x) = x
T_n+1(x) = 2xT_n(x) - T_n-1(x)
U₀(x) = 1
U₁(x) = 2x
U_n+1(x) = 2xT_n(x) - T_n-1(x)

Unit description

The recurrence relation given above is the most efficient way to calculate the Chebyshev polynomial. The ChebyshevCalculate subroutine uses this relation to calculate T_n(x) and/or U_n(x) for any given x.

The ChebyshevSum subroutine calculates the sum of Chebyshev polynomials c₀T₀(x) + c₁T₁(x) + ... + c_nT_n(x) using Clenshaw's recurrence formula.

The ChebyshevCoefficients subroutine can represent T_n(x) as a sum of powers of x: c₀ + c₁x + ... + c_nxⁿ.

The FromChebyshev subroutine can perform a conversion of a series of Chebyshev polynomials to a power series.

This article is licensed for personal use only.

Download ALGLIB for C++ / C# / Java / Python / ...

ALGLIB Project offers you two editions of ALGLIB:

ALGLIB Free Edition:
+delivered for free
+offers full set of numerical functionality
+extensive algorithmic optimizations
-no multithreading
-non-commercial license

ALGLIB Commercial Edition:
+flexible pricing
+offers full set of numerical functionality
+extensive algorithmic optimizations
+high performance (SMP, SIMD)
+commercial license with support plan

Links to download sections for Free and Commercial editions can be found below: