Gaussian quadrature

Consider the calculation of the following integral:

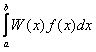
where a, b and W(x) are known in advance. There are two ways of calculating this integral. The first way is to use one of the common integration algorithms (Simpson's, Romberg's, etc). The second way includes the optimal choice of the node location and weight factor values of the quadrature formula (taking into account the integration interval and the W(x) function) to achieve the maximum possible accuracy with the given number of nodes N. The quadrature formula built in such a way is called the Gaussian quadrature formula. If f is a polynomial with power not higher than 2·N-1, the Gaussian quadrature allows for calculating the exact integral value.

Types of Problems

Calculation tasks connected with building Gaussian quadrature formulas can be divided into three categories: 1) important separate cases (Gauss-Legendre, Gauss-Jacobi, Gauss-Hermite, Gauss-Laguerre quadratures); 2) problems with arbitrary W(x); 3) problems with arbitrary W(x) and preset location of one or two nodes (usually on the borders of the integration range).

When solving problems of the first type only weight function class and its parameters are required. Problems of second and third type are more difficult as the weight function have general form and it is required to express its properties numerically. Traditionally for this purpose one uses the coefficiants of a recurrent formula that induces a sequence of orthogonal polynomials (if the terminology is not familiar, see for example chapter 4.5 Numerical Recipes).

Algorithm

To calculate the nodes and weight factors an algorithm is used that converts the problem of building a quadrature formula into the task of finding eigenvalues and eigenvectors of tridiagonal matrix. A tridiagonal matrix is built on the basis of coefficients of recurrent formula. The eigenvalues of the matrix are nodes of the formula and the first line of the eigenvectors matrix represents the weight factors. The algorithm and matrix structure for each of the quadrature types (Gauss, Gauss-Radau and Gauss-Lobatto) are described in more detail in the "Orthogonal polynomials and quadrature", W. Gautschi, 1999.

Limitations

Building a Gauss quadrature formula has a complexity of O(N²) (where N is the number of nodes), i.e. the increase of N leads to an increase in time required for quadrature building. Moreover, with the increase of N the inaccuracy of finding the nodes/factors also increases. Finally, the quadrature formulas with large node numbers have high requirements for the f(x) smoothness (the W(x) function may not be smooth). This is why the quadrature formulas with number of nodes larger than 100-1000 are used rarely. Most often the formulas with a small number of nodes (3-50) are used.

This article is licensed for personal use only.