Hierarchical clustering

Cluster analysis is a task of partitioning set of N objects into several subsets/clusters in such a way that objects in the same cluster are similar to each other. ALGLIB package includes several clustering algorithms in several programming languages, including our dual licensed (open source and commercial) flagship products:

• ALGLIB for C++, a high performance C++ library with great portability across hardware and software platforms
• ALGLIB for C#, a highly optimized C# library with two alternative backends: a pure C# implementation (100% managed code) and a high-performance native implementation (Windows, Linux) with same C# interface

Our implementation of clustering algorithms is highly optimized and feature rich (see below for more complete discussion):

• agglomerative clustering algorithms and k-means
• various distance metrics (L0, L2, Linf, correlation, cosine, distance matrix)
• various linkage types (SLINK, CLINK, Ward)
• algorithmic and low-level optimizations, including parallelism and SIMD support

Agglomerative hierarchical clustering

General information

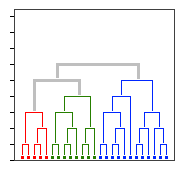
Agglomerative hierarchical clustering (AHC) is a popular clustering algorithm which sequentially combines smaller clusters into larger ones until we have one big cluster which includes all points/objects.

Problem statement includes set of points/objects; metric (formula which is used to determine distance between two points); linkage type (formula which is used to determine distance between two clusters).

We start from N single-point clusters and, according to chosen linkage type, we choose two closest clusters and merge them into one larger cluster. Previous step is repeated until all clusters are merged into one big cluster. As result, we get dendrogram which can be used to quickly get top K clusters for any given K.

Benefits of such approach to clustering are:

• ability to use any metric
• ability to choose between many linkage types
• user may work with top K clusters for any given K - or may work with full dendrogram

Drawbacks are are:

• O(N²) memory requirements (algorithm have to store several copies of NxN distance matrix), which makes algorithm applicable only to medium scale problems (up to 10.000 points). Large-scale problems can not be solved because of memory limits.
• O(N²·M) working time (where M is a number of features)

Metric types

Agglomerative hierarchical clustering algorithm may work with many different metric types. Following metrics are supported:

• classic Euclidean L2
• Chebyshev L-inf
• Manhattan (city-block) L0
• Pearson correlation (including absolute correlation)
• cosine metric (including absolute cosine metric)
• Spearman's correlation (including absolute correlation)

Metric is chosen during addition of the dataset with clusterizersetpoints. You may also work with dataset specified by distance matrix - without explicitly specifying points and metric. In the latter case you should use clusterizersetdistances function to specify your dataset.

Linkage types

Metric is a formula which defines distance between two points. But we also need some formula to determine distance between two clusters A and B, each of them having several points.

Formula which defines distance between clusters is called "linkage type", and algorithm results are greatly influenced by chosen linkage type. ALGLIB supports several linkage types:

• complete linkage: dist(A,B) = max(dist(a,b) : a in A, b in B).
• single linkage: dist(A,B) = min(dist(a,b) : a in A, b in B).
• unweighted average linkage: dist(A,B) = average(dist(a,b) : a in A, b in B)
• weighted average linkage.
• Ward's method.

By default, complete linkage is used because it gives best results (robustness, quality of the clusters).

Examples

ALGLIB Reference Manual includes several examples on AHC:

• clst_ahc - simple clustering with default settings
• clst_distance - clustering with different metrics
• clst_linkage - clustering with different linkage types
• clst_kclusters - working with dendrogram

Performance and multi-core support

In this section we compare performance of two ALGLIB editions - Free and Commercial. All tests were performed on six-core AMD Phenom II X6 CPU running at 3.1 GHz, with one core left unused to leave system responsive. Following products were compared:

• managed core, Free Edition  -  100% NET code, C# interface.
• managed core, Commercial Edition - 100% NET code with multithreading support, C# interface.
• native core, Free Edition - generic C native code, C++ interface (no C# interface!).
• native core, Commercial Edition - highly optimized native core with multithreading support, accelerated by Intel MKL, C++ and C# interfaces.

During testing we compare running times for different computational cores on two kinds of problems. Algorithm running time is a sum of two terms: time to build distance matrix and time to form clusters. For a problem with N points, each of them having M features, first stage (distance matrix) needs O(M·N²) time, and second one needs O(M²) time. Second stage can be parallelized, while the second one is inherently sequential. Charts below show algorithm total running time and separate times for first and second stages.

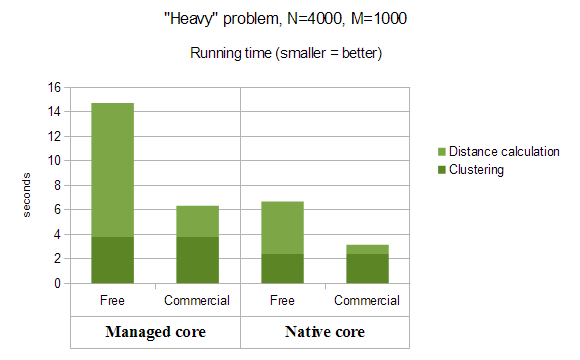
First benchmark was performed on random clustering problem with N=4000 points and M=1000 features, and Euclidean metric. We called this problem "heavy" because it has many features (M=1000), and running time was dominated by distance matrix calculation - it takes 75% of CPU time, and only 25% were used for the clustering itself.

You may see that Commercial Edition of ALGLIB do its best on this problem: we have more than 2x speed-up from going multithreaded (from Free Edition to Commercial one) for both kinds of computational cores - managed and native. And if you work in C#, you may get additional 2x speedup from moving to native computational core, which is present only in Commercial Edition of ALGLIB for C#, which results in 4-5x overall increase in speed.

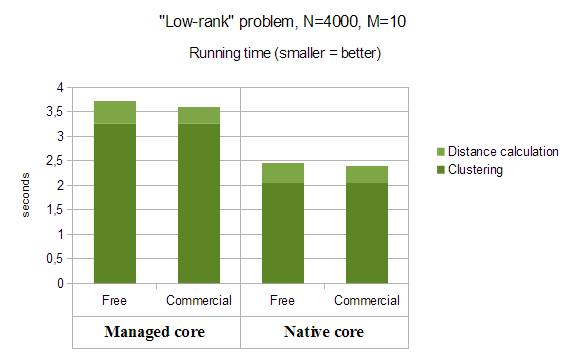
Second benchmark was performed on so called "low rank" problem with large amount of points (N=4000), but just 10 features. On this problem only 15% of the algorithm running time was spent in distance calculation, and 85% of time was spent in the clustering phase, which is inherently sequential.

You may see that on clustering problems with small amount of variables you will get almost negligible speedup from multithreading or other straightforward optimizations. For each of the computational cores, Free Edition performs almost equally as well as Commercial one. However, if you use Commercial Edition of ALGLIB for C#, you may switch from managed core to native one and get about 30% speedup.

k-means clustering

General information

K-means clustering is another popular clustering algorithm. Despite being quite old, it is still widely used for solution of large-scale clustering problems.

Short description of algorithm is given below:

• we have N points, each of them with M features, number of clusters K is fixed
• algorithm selects initial cluster centers (k-means++ initialization algorithm is used for cluster selection)
• each point is assigned to nearest cluster (cluster with nearest center; Euclidean metric is used)
• cluster centers are updated (set to mean of all points in the cluster)
• last two steps are repeated until convergence (cluster centers do not change) - or until specified number of iteration is performed

Benefits of the k-means algorithm are:

• simple and straightforward algorithm which is easy to optimize
• due to moderate O(K·M) memory requirements and O(K·M·N) iteration cost, k-means algorithm is fast and compact, and can be used on large-scale problems

However, this algorithm has following drawbacks:

• it works only with Euclidean metric
• number of clusters K is fixed and must be chosen by user; inappropriate K may yield misleading results
• running time of the algorithm is unbounded, although on real-life problems it usually works well

Examples

ALGLIB Reference Manual includes following examples on k-means algorithm:

• clst_kmeans - simple k-means clustering

This article is licensed for personal use only.