
The Legendre polynomials, sometimes called Legendre functions of the first kind, are defined as solutions of Legendre's differential equation:
Solutions corresponding to the non-negative integer n can be expressed using Rodrigues' formula
or can be constructed using the three term recurrence relation:
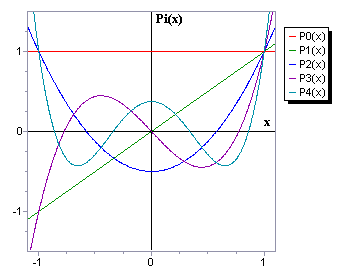
P0(x) = 1The recurrence relation given above is the most efficient way to calculate the Legendre polynomial. The LegendreCalculate subroutine uses this relation to calculate Pn(x) for any given x.
The LegendreSum subroutine calculates the sum of Legendre polynomials c0P0(x) + c1P1(x) + ... + cnPn(x) using Clenshaw's recurrence formula.
The LegendreCoefficients subroutine can represent Pn(x) as a sum of powers of x: c0 + c1x + ... + cnxn.
This article is licensed for personal use only.
ALGLIB Project offers you two editions of ALGLIB:
ALGLIB Free Edition:
+delivered for free
+offers full set of numerical functionality
+extensive algorithmic optimizations
-no multithreading
-non-commercial license
ALGLIB Commercial Edition:
+flexible pricing
+offers full set of numerical functionality
+extensive algorithmic optimizations
+high performance (SMP, SIMD)
+commercial license with support plan
Links to download sections for Free and Commercial editions can be found below:




