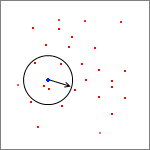
Nearest neighbor search

Nearest neighbor search is an important task which arises in different areas - from DNA sequencing to game development. One of the most popular approaches to NN searches is k-d tree - multidimensional binary search tree.

ALGLIB package includes highly optimized k-d tree implementation available in several programming languages, including:

• ALGLIB for C++, a high performance C++ library with great portability across hardware and software platforms
• ALGLIB for C#, a highly optimized C# library with two alternative backends: a pure C# implementation (100% managed code) and a high-performance native implementation (Windows, Linux) with same C# interface

Our implementation of k-d trees includes following features (see below for more detailed discussion):

• high-performance C++/C# code scalable to big data loads
• various kinds of queries: k nearest neighbors, all neighbors within R-sphere, approximate k-NN, box queries
• flexible interface with ability to attach Y-values and tags to dataset points

Getting started and examples

Getting started

K-d tree functionality (and nearest neighbor search) are provided by the nearestneighbor subpackage of ALGLIB package. Everything starts with k-d tree model creation, which is performed by means of the kdtreebuild function or kdtreebuildtagged one (if you want to attach tags to dataset points). This function initializes an instance of the kdtree class, which can be used to perform various kinds of activities.

Depending on specific task being solved, you can:

• create k-d tree with just X-values (point locations) being stored in the structure
• additionally, store Y-values in the structure, NY ones per point (Y-values can be values of some function, dataset labels, and so on)
• additionally, store integer tags in the structure (tags can be used to identify point locations in the external database/array/...)

After k-d tree is built, you can perform various kinds of spatial queries:

• get k nearest neighbors with kdtreequeryknn function
• get k approximate nearest neighbors with kdtreequeryaknn function
• get all neighbors within specified radius with kdtreequeryrnn function
• get all neighbors within a box with kdtreequerybox function

Examples

We prepared several examples (in C++, C# and all other programming languages supported by ALGLIB) of k-NN searches with ALGLIB:

• nneighbor_d_1 - how to build k-d tree, perform query and extract results
• nneighbor_d_2 - how to serialize/unserialise k-d trees

Sections below discuss these examples in more details.

k-d trees in ALGLIB

Some theory

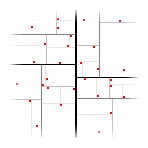
K-d trees are data structures which are used to store points in k-dimensional space. As it follows from its name, k-d tree is a tree. Tree leafs store points of the dataset (one or several points in each leaf). Each point is stored in one and only one leaf, each leaf stores at least one point.

Tree nodes correspond to splits of the space (axis-oriented splits are used in most implementations). Each split divides space and dataset into two distinct parts. Subsequent splits from the root node to one of the leafs remove parts of the dataset (and space) until only small part of the dataset (and space) is left.

Chart at the right shows an example of k-d tree in the 2-dimensional space. Red squares are dataset points, black lines are splits. The thinner the line is, the deeper is the node which corresponds to the split.

k-d trees allow to efficiently perform searches like "all points at distance lower than R from X" or "k nearest neighbors of X" in low-dimensional spaces. However, their efficiency decreases as dimensionality grows, and in high-dimensional spaces k-d trees give no performance over naive O(N) linear search (although continue to give correct results).

Considering number of dimensions K fixed and low, and dataset size N variable, we can estimate complexity of the most important operations with k-d tree:

• building a k-d tree has O(N·logN) time complexity and O(K·N) space complexity
• nearest neighbor search - close to O(logN)
• M nearest neighbors - close to O(M·logN)

Creating k-d tree object

ALGLIB implementation of k-d trees uses following dataset model:

• dataset S includes N points in NX-dimensional space. Coordinates in NX-dimensional space of points are called X-values.
• points may have additional attributes: Y-values and/or integer tags. These attributes may be returned with X-values as the query result.
• Y-values are NY real numbers associated with point. Y-values are not used for distance computation. Usually it is value of some NY-dimensional vector function at the point.
• Tag is an integer number associated with point (say, its index in the external array of database).
• X-values, Y-values and tags are passed to k-d tree when it is built from dataset.

k-d trees are built with one of the constructor functions: kdtreebuild or kdtreebuildtagged. First one builds k-d tree without tags (but with optional Y-values), second one builds k-d tree with tags (and with optional Y-values). As result, these functions return kdtree structure.

Queries: k-NN, R-NN, AKNN, box queries

After tree is built, you can perform several kinds of queries:

• KNN-queries - find K nearest neighbors of X.
• AKNN-queries - find K ε-approximate nearest neighbors with given degree of approximation. Such queries are several times faster than exact KNN queries, especially in high dimensional spaces.
• RNN-queries - find all points at distance R or closer.
• box queries - find all points at distance R or closer.

NN searches are performed in two stages. At the first stage we send a query using one of the querying functions: kdtreequeryknn, kdtreequeryaknn, kdtreequeryrnn or kdtreequerybox. These functions perform search, save result in the internal buffers of the kdtree structure, and return result size (number of points satisfying search criteria).

At the second stage user may extract result by calling one of the functions: kdtreequeryresultsx to get X-values, kdtreequeryresultsxy to get X and Y-values, kdtreequeryresultstags to get tags, kdtreequeryresultsdistances to get distances from dataset points to X.

ALGLIB Reference Manual contains nneighbor_d_1 example which shows how to work with k-d trees.

Thread-safe interface

Querying functions listed above save their results in the internal buffers of the k-d tree structure. It is very convenient... until you decide to send queries from several threads. Any attempt to work with same k-d tree object from multiple threads will result in corruption of its internal data structures. However, ALGLIB has a solution designed for such cases - thread-safe interface.

Thread-safe interface to k-d trees uses k-d tree instance in read-only mode and stores query results (and temporaries) in the special structure: kdtreerequestbuffer. Every thread should maintain its own independent copy of the request buffer. As long as different threads use separate request buffers, working with k-d tree is thread-safe.

Following functions perform thread-safe queries (note: ts prefix indicates that it is thread-safe):

• kdtreetsqueryknn
• kdtreetsqueryaknn
• kdtreetsqueryrnn
• kdtreetsquerybox

Functions below retrieve results from request buffers:

• kdtreetsqueryresultsx
• kdtreetsqueryresultsxy
• kdtreetsqueryresultstags
• kdtreetsqueryresultsdistances

Serialization/unserialization

kdtreeserialize and kdtreeunserialize functions can be used to serialize k-d tree (convert it to string or stream) and unserialize it (restore structure from string/stream representation). Serialization allows to save tree to file, move between different computers and even versions of ALGLIB in different programming languages.

ALGLIB Reference Manual includes an example on serialization of k-d trees - nneighbor_d_2.

Benchmarks

In order to estimate performance of ALGLIB implementation of k-d trees we've conducted a series of numerical experiments. Experiments were performed on AMD Phenom II X6 3.2GHz CPU with Microsoft C++ compiler and maximum optimization settings. During experiments we've generated N=50.000 points, uniformly and randomly distributed across D-dimensional unit hypercube. Then we performed 50.000 queries for K nearest neighbors.

Depending on number of dimensions K, k-d tree construction took from 30 to 60 ms. Approximate time complexity is O(D·N·logN), i.e. construction time is linear with respect to number of dimensions and linearithmic with respect to dataset size.

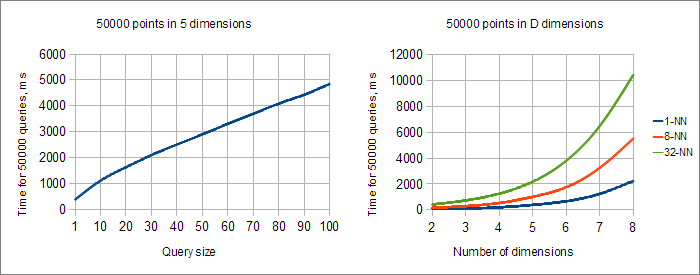
Charts above show how query processing time depends on number of neighbors K and number of dimensions D. From the first chart we can conclude that KNN query time grows approximately linearly with respect to K (the best result possible).

Second chart allows to study performance of k-d tree in connection with number of dimensions D. You may see that for any K (even for K=1) query time exponentially grows as we increase number of dimensions. Each additional dimension results in approximately 1.7-fold increase of processing time. In high dimensional spaces we have to scan more leafs of the tree, and at some moment k-d tree will become just complicated form of linear search (all nodes are examined). BTW, at this point query time will stop to grow exponentially with growth of D.

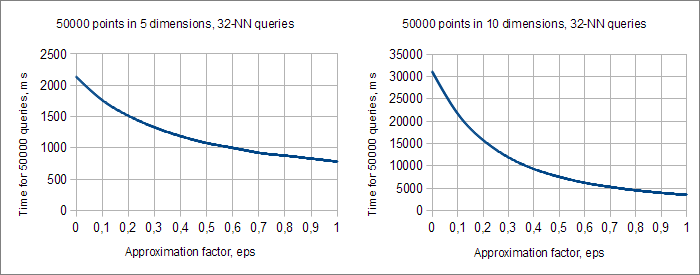
One of the ways to fight "curse of dimensionality" is to use approximate (AKNN) queries. When we process ε-approximate KNN query we can return inexact nearest neighbor, located at distance r·(1+ε) from X} (where r is a distance to true nearest neighbor). The larger approximation factor ε we choose, the more leafs can be skipped when we scan the tree.

Charts above show time complexity of AKNN-queries with different values of the approximation factor ε and different number of dimensions D. You may see that the higher D we choose, the more advantageous is to use AKNN queries. With D=5 and ε=1 AKNN queries give us only 3-fold increase of performance, but D=10 and ε=1 give us 10-fold increase.

Obviously, approximate KNN queries are not universal solution. In many cases we have to know exact nearest neighbors. However, in some areas (like large scale data processing) it is sufficient to work with inexact results.

This article is licensed for personal use only.