Constrained quadratic programming

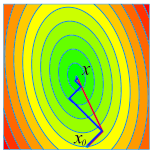
Quadratic programming is a subfield of nonlinear optimization which deals with quadratic optimization problems subject to optional boundary and/or general linear equality/inequality constraints:

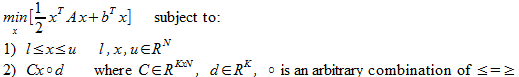
Quadratic programming problems can be solved as general constrained nonlinear optimization problems. However, because we know that function being optimized is quadratic one, we can use specialized optimization algorithms which are more precise and robust that general ones.

ALGLIB package provides several state-of-the-art QP solvers which can solve convex and non-convex problems, dense and sparse, box-constrained and linearly constrained ones. This article discusses these solvers and their properties. We will also review minqp subpackage which is used to solve constrained quadratic programming problems.

Note #1
This article complements ALGLIB Reference Manual - a technical description of all ALGLIB functions with automatically generated examples. If you want to know what functions to call and what parameters to pass, Reference Manual is for you. Here, in ALGLIB User Guide, we discuss ALGLIB functionality (and optimization in general) in less technical manner. We discuss typical problems arising during optimization, mathematical algorithms implemented in ALGLIB, their strong and weak points - everything you need to get general understanding of quadratic optimization.

Quadratic programming overview

Iterative and factorization-based approaches

All QP solvers are iterative - except for the very basic unconstrained case, QP problem can not be solved in one step. However, it is possible to informally classify QP solvers as "purely iterative" and "factorization-based". Former perform iterations of some nonlinear optimizer (usually CG or LBFGS). These methods heavily rely on just one operation with quadratic term - matrix-vector product, which is used to evaluate gradient of target function.

Factorization-based methods are different - they use Cholesky decomposition (other factorizations are rarely used) of quadratic term to perform iterations. Such approach has several advantages. First, it is more robust than "purely iterative" approach. Second, one step of factorization-based method usually results in significant improvement in function value - comparable to N steps of "purely iterative" method. Finally, because factorization is usually performed with Level 3 BLAS, it is fast and cache-efficient.

From the other side, Cholesky-based methods have limited use on indefinite (non-convex) QP problems. It does not mean that these methods are completely useless - non-convex problem is often "convexified" by constraints. But their performance may significantly decrease. Another drawback of factorization-based methods is that sometimes you can not afford factorization because of memory constraints (say, when you solve sparse problem which has prohibitively large Cholesky decomposition). Speaking shortly, both families of methods have benefits and drawbacks, and good optimization package (like ALGLIB) should implement both of them.

Convex (positive definite), semidefinite and indefinite QP problems

One of the most important classifications of QP problems rely on properties of the quadratic term A: whether it is positive definite, semidefinite or indefinite:

• Positive definite QP problems are the most easy ones. First reason is that they are strictly convex, which results in one and only one global minimum. Second reason is that convexity makes solution process more robust. Last but not least is that we can use Cholesky decomposition to speed-up solution process.
• Semidefinite problems are a bit harder to solve. Unconstrained semidefinite problem has infinitely many (affine subspace) solutions. Solution process becomes less robust because optimizer is likely to start "sliding" along this subspace, to perform large steps which do not change function value. However, even small amount of regularization (applied automatically by ALGLIB) "cures" problem and makes it positive definite.
• Indefinite QP problems are the hardest ones. They have solution only under constraints - unconstrained problem is unbounded from below. Cholesky-based methods can not be used because of matrix properties. Regularization does not help to solve issue with Cholesky decomposition because minor regularization has no effect whilst larger regularization slows down convergence - optimizer performs gradient descent steps instead of Newton steps. ALGLIB can solve even indefinite problems, but at the cost of lesser performance.

Constraints

All constrained optimizers (quadratic or not) can be informally divided into three categories: active set methods, barrier/penalty methods, Augmented Lagrangian methods:

• Active set methods handle constraints analytically, always performing strictly feasible steps. Constraints are satisfied almost exactly (close to machine precision). These methods are quite stable on noise-free problems, but sometimes they are too sensitive to rounding noise.
• Barrier/penalty methods handle constraints by modification of the target function - they add some form of penalty for crossing (or approaching to) boundary of the constrained area. It means that constraints are enforced approximately - there always exists significant non-zero violation of constraints. Say, on unit-scale problem it is normal to have violation of constraints as large as 0.01 (error in the solution has same magnitude).
• Augmented Lagrangian (AUL) methods are important improvement of barrier/penalty methods. They use penalty for violation of constraints, and they have one more term which is added to target function - shift term for fine-tuning of constraints. Augmented Lagrangian methods usually achieve moderate precision - say, on unit-scale problem you may achieve error in the solution/constraints as low as 0.000001.

Charts above show behavior of typical active set (first chart) and penalty methods (second one). Active set method handles constraints exactly - changes search direction exactly at the boundary of the feasible set. Penalty method performs steps which violate constraints. Active set method requires less iterations and finds minimum with higher precision, but has higher iteration cost.

QP solvers provided by ALGLIB

QP-BLEIC solver

QP-BLEIC is a Boundary and Linear Equality-Inequality Constrained QP solver, which is a thin wrapper around general purpose BLEIC optimizer - another ALGLIB optimizer with similar name. This optimizer can solve convex and indefinite, dense and sparse QP problems with box and general linear constraints. It can be considered as "default solution", which always works, albeit slower than specialized methods.

This solver can be classified as purely iterative (no factorization) active set (exact handling of constraints) method. Being purely iterative, it relies on matrix-vector products with quadratic term as the only way of working with target function. Because it is active set method, QP-BLEIC enforces constraints exactly, always performing feasible steps. QP-BLEIC solver can be used to solve large-scale quadratic programming problems (N=thousands or tens of thousands).

The most important limitation of solver is that it is intended for problems with moderate amount of non-box (general linear) constraints. Being active set method, QP-BLEIC has to store and update set of orthogonalized constraints, which costs O(N·K²) FLOPS for N-dimensional problem with K active non-box constraints. Thus, method is pretty fast for 10000-dimensional problem with 10 non-box constraints, but becomes prohibitively slow when constraints count increases to 1000. From the other side, box constraints are handled very efficiently, with almost negligible overhead. Less important limitation is that constraints are always activated one-by-one, i.e. if solution has 100 active constraints, solver will have to perform at least 100 steps.

QuickQP solver

QuickQP is a specialized QP solver for very efficient solution of box-constrained (no general linear constraints!) dense and sparse QP problems. This solver can work with indefinite problems, although it is optimized for convex/semidefinite ones. It is tens of times faster than QP-BLEIC solver.

This solver can be classified as active set method with fast activation of constraints (up to hundreds per iteration), iterative main phase (constrained CG) and additional factorization-based stage (constrained Newton). This method works amazingly fast and in many cases can solve 1000-dimensional problem in just 10 iterations.

The only limitation of the method is that it can not solve problems with general linear constraints - its constraints activation code can work only with box constraints.

Solving quadratic programming problems with ALGLIB

minqpstate object

As all ALGLIB optimizers, minqp unit is built around minqpstate object. You should use it for everything QP-related - from problem specification to retrieval of results:

1. create instance of optimizer with minqpcreate function
2. choose one of the QP algorithms by means of appropriate function (minqpsetalgobleic or minqpsetalgoquickqp), stopping criteria are usually specified at this stage
3. pass to optimizer problem specifications like quadratic/linear terms, constraints, scale of variables
4. start optimizer with minqpoptimize function
5. retrieve results with minqpresults function

Choosing algorithm

One of the most important choices is to choose appropriate QP solver. minqp unit provides several QP solvers with different properties. Default option is to use QP-BLEIC - general purpose QP solver which can be used for dense/sparse problems with arbitrary mix of box and general linear constraints. This solver is purely iterative and is suited for high-dimensional quadratic programming problems (as long as they have moderate amount of general linear constraints).

Scale of the variables

Before you start to use optimizer, we recommend you to set scale of the variables with minqpsetscale function. Variable scaling is essential for correct work of the stopping criteria (and sometimes for convergence of optimizer). You can do without scaling if your problem is well scaled. However, if some variables are up to 100 times different in magnitude from their neighbors, we recommend you to tell solver about their scale. And we strongly recommend to set scaling in case of larger difference in magnitudes.

We recommend you to read separate article on variable scaling, which is worth reading unless you solve some simple toy problem.

Stopping criteria

ALGLIB package offers four kinds of stopping conditions:

• gradient-based - scaled gradient norm is small enough (scaled gradient is a gradient which is component-wise multiplied by vector of the variable scales)
• stepsize-based - scaled step norm is small enough (scaled step is a step which is componentwise divided by vector of the variable scales)
• function-based - function change is small enough
• iteration-based - after specified number of iterations

You can set one or several conditions at the moment you choose QP algorithm. After algorithm termination you can examine completion code to determine what condition was satisfied at the last point.

Note #2
You should not expect that algorithm will be terminated by and only by stopping criterion you've specified. For example, algorithm may take step which will lead it exactly to the function minimum - and it will be terminated by first criterion (gradient norm is zero), even when you told it to "make 100 iterations no matter what".

Note #3
Some stopping criteria use variable scales, which should be set by separate function call.

Examples

ALGLIB Reference Manual includes following examples:

• minqp_d_bc1 - example on box constrained optimization with QuickQP and QP-BLEIC solvers
• minqp_d_lc1 - example on linearly constrained optimization with QP-BLEIC solver
• minqp_d_nonconvex - example on nonconvex optimization
• minqp_d_u1 - example on unconstrained dense optimization
• minqp_d_u2 - example on unconstrained sparse optimization

Performance

Bound constrained problems

Box constrained QP problems can be solved with two QP algorithms: QP-BLEIC and QuickQP. First one is a general purpose active set method applied to quadratic programming. Second method is an active set algorithm, specialized in solution of box-constrained problem.

QuickQP algorithm includes several improvements over traditional active set methods: 1) fast activation of multiple constraints in one step, 2) hybrid algorithm which combines iterations of constrained conjugate gradient and iterations of constrained Newton method 3) improved constrained Newton method which reuses/updates Cholesky factorization of the quadratic term.

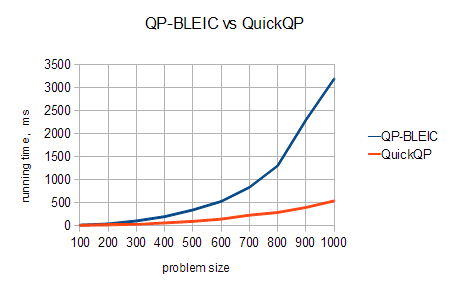
Chart above allows us to see comparative performance of these two methods. We solve multiple dense convex QP problem subject to box constraints and calculate average time required for solution. All QP algorithms use same stopping criteria. A sequence of different problems sizes in [100,1000] is tried. Time required to solve problem was measured on a modern 3.2GHz CPU, with native computational core.

It is easy to see that QuickQP solver consistently outperforms QP-BLEIC. What it interesting is that for small N (100...500) it is 3-4 times faster, but difference in performance steadily increases as N grows. For N=1000, QuickQP is 6 times faster than QP-BLEIC.

One reason for such difference is that QuickQP uses Newton iteration combined with fast activation of box constraints. It needs less iterations to converge than BLEIC-based solver. Another reason is that QuickQP algorithm is more cache friendly than QP-BLEIC - former heavily relies on Cholesky factorization, which is done with cache-efficient algorithm, while for latter core operation is matrix-vector product, which has low cache efficiency for large matrices.

Linearly constrained problems

QP problems with general linear (non-box) constraints can be solved with QP-BLEIC solver. As we told before, QP-BLEIC is an active set method which handles constraints analytically. Exact handling of constraints results in more precise solutions, but it has one important downside. Cost of handling K constraints grows as N·K² per step, where N is a problem dimension.

You should keep in mind performance profile of QP-BLEIC algorithm when preparing to solve quadratic programming problem. It is recommended to reformulate constraints as boundary when possible. High-dimensional problem with moderate amount of general linear constraints can be solved relatively fast, but when constraints count grows to thousands, solution process becomes impractically slow.

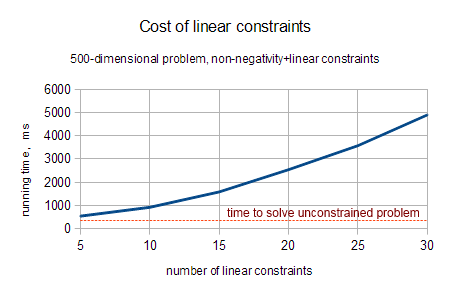
Chart above shows time required to solve same 500-dimensional QP problem with different number of linear constraints. Test was performed on 3.2GHz CPU, with native computational core.

.NET vs native computational core

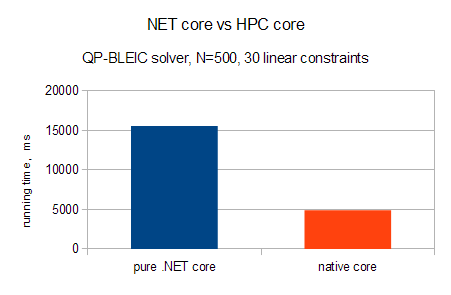
ALGLIB package is distributed in several versions: C++ version, C# version, versions in other language. ALGLIB for C# has one distinguishing feature - commercial edition of the package has two different computational cores, each with 100% identical API. It allows commercial users to easily switch between 100% managed version written in pure C# - and high-performance version (native code, Intel MKL) with same functionality. Chart below shows that native core is about 3 times faster than the pure NET version.

Note #4
Open source users do not have access to high-performance computational core. However, managed computational core provides same functions - just slower.

This article is licensed for personal use only.