About preconditioning

    1 Preconditioner
           Example
           When do you need preconditioner
           Preconditioners supported by ALGLIB

Preconditioner

Preconditioning is a transformation which transforms optimization problem into a form more suitable to solution. Usually this transformation takes form of the linear change of the variables - multiplication by the preconditioner matrix. The most simple form of the preconditioning is a scaling of the variables (diagonal preconditioner) with carefully chosen coefficients.

Example

Below you can find an example of the preconditioner accelerating convergence. Original function is a narrow valley and optimizer bounces off the walls of the valley while approaching to the solution. Finally, it arrives to the isoline f=1, but it needs 4 iterations to reach it. After the scaling curvature of the function became more simple and we need only one step in order to move far below f=1.

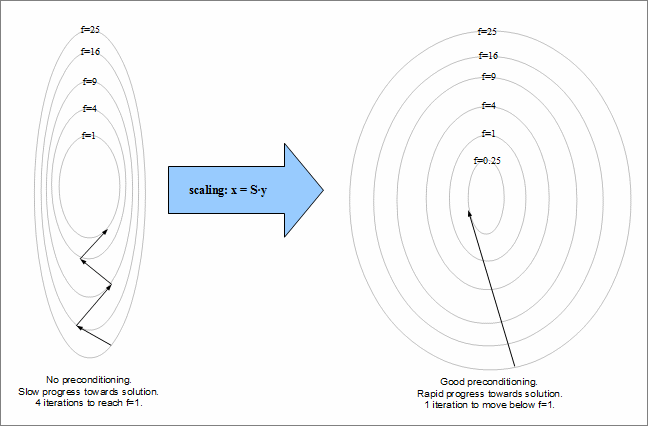
In the example above we used very basic optimization algorithm - steepest descent method. You can understand it by noticing that steps are always made in the direction of the antigradient, without accumulating information about curvature of the function. Both L-BFGS and CG would have started to turn search direction toward extremum right after the first iteration. But it does not mean that good optimization algorithm does not need preconditioner. Good preconditioner can significantly (up to several times) speed up optimization progress.

When do you need preconditioner

You will need preconditioner if:

your variables have wildly different magnitudes (thousand times and higher)
your function rapidly changes in some directions and slowly - in other ones
analysis of Hessian matrix suggests that your problem is ill-conditioned
you want to accelerate optimization

Sometimes preconditioner just accelerates convergence, but in some difficult cases it is impossible to solve problem without good preconditioning.

Preconditioners supported by ALGLIB

ALGLIB package supports several preconditioners:

default one, which does nothing (just identity transform).
diagonal Hessian-based preconditioner. In order to use this preconditioner you have to calculate diagonal of the approximate Hessian (not necessarily exact Hessian). Diagonal matrix must be positive definite - algorithm will throw an exception on matrix with zero or negative elements on the diagonal. This preconditioner can be used for convex functions, or in situations when function is possibly non-convex, but you can guarantee that approximate Hessian will be positive definite.
diagonal scale-based preconditioner. It can be used when your variables have wildly different magnitudes, which makes it hard for optimizer to converge. In order to use this preconditioner you should set scale of the variables (see article about scaling).

Different optimizer support different types of preconditioners, but first three are supported by all ALGLIB optimizers.

This article is intended for personal use only.