Bound and linear equality/inequality constrained optimization

This article discusses minbleic subpackage - optimizer which supports boundary and linear equality/inequality constraints. This subpackage replaces obsolete minasa subpackage. BLEIC algorithm (boundary, linear equality-inequality constraints) can solve following optimization problems:

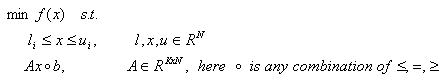
Contents     1 About algorithm            BLEIC as active set algorithm            Additional information     2 Starting to use algorithm            Choosing between analytic and exact gradient            Scale of the variables            Preconditioner            Stopping conditions            Constraints     3 Examples

About algorithm

BLEIC as active set algorithm

Active set algorithm is a name for a family of methods used to solve optimization problems with equality/inequality constraints. Method name comes from the classification of constraints, which divides them into active at the current point and inactive ones. The method reduces equality/inequality constrained problem to a sequence of equality-only constrained subproblems. Active inequality constraints are treated as equality ones, inactive ones are temporarily ignored (although we continue to track them).

Informally speaking, current point travels through feasible set, "sticking" to or "unsticking" from boundaries. Image below contains example for some problem with three boundary constraints:

1. we start from the initial point, where all constraints are inactive
2. we solve first (unconstrained) subproblem and arrive at (0,1), where we activate constraint (1)
3. second subproblem leads us to (0,0), where we "stick" to the boundary
4. we activate constraint (3) and deactivate constraint (1)
5. finally, we arrive to (1,0), where algorithm stops

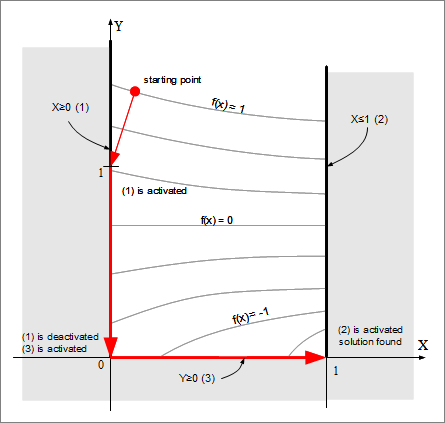
The most important feature of active set family is that active set method is easy to implement for problems with linear constraints. Equality-constrained subproblems can be easily solved by projection onto subspace spanned by active constraints. In the linear case active set method outperforms its main competitors (penalty, barrier or modified Lagrangian methods). In particular, constraints (both boundary and linear) are satisfied with much higher accuracy.

Additional information

In this section we'll consider key features of the BLEIC algorithm (implemented by minbleic subpackage). Below we'll use following notation: N will denote number of variables, K will denote number of general form linear constraints (both equality and inequality ones), Ki will denote number of general form inequality constraints.

Following properties should be noted:

• we use nonlinear conjugate gradient method as underlying optimization algorithm
• equality constraints are handled by projection of the target function onto equality-constrained subspace
• inequality constraints are handled by activation/deactivation (i.e. by treating them as equality ones, if necessary, or dropping from consideration otherwise)
• current version of the BLEIC algorithm does not support modification of the preconditioner on the fly. You can change it during algorithm iterations, but it won't take effect until restart of the algorithm.
• algorithm modifies problem by addition of the slack variables to linear (non-boundary) inequality constraints. As result, the only inequality constraints we have are boundary ones. All linear inequality constraints are transformed into equality ones plus one additional boundary constraint (non-negativity) for the slack variable.
• boundary constraints are handled separately from the general linear ones as important special case. Boundary constraints have lower computational overhead and are always satisfied exactly - both in the final point and in all intermediate points. For example, in case of non-negativity constraint we won't even evaluate function at points with negative x.
• general form linear constraints (both equality and inequality ones) require more time than boundary ones. Both equality and inequality constraints can be satisfied with small error (about N·ε in magnitude). For example, with x+y≤1 as constraint we can stop at the point which is slightly beyond x+y=1 (about N·ε away from the feasible set).
• constraints add computational overhead. Additional computations are required at two moments: when we activate/deactivate constraints and when we evaluate target function. When we activate/deactivate even one constraint we have to reorthogonalize constraint matrix, which will require O((N+Ki)·K ²) operations. Every evaluation of the target function will require O(N) additional operations for boundary constraints and O((N+Ki)·K) operations for linear ones.
• Computational overhead for handling constraint is almost independent of whether it is active or not. The only situation when computational overhead is insignificant is when we have boundary constraint like -∞<x or x<+∞.

Starting to use algorithm

Choosing between analytic and exact gradient

Before starting to use L-BFGS/CG optimizer you have to choose between numerical diffirentiation or calculation of analytical gradient. For example, if you want to minimize f(x,y)=x ²+exp(x+y)+y ², then optimizer will need both function value at some intermediate point and function derivatives df/dx and df/dy. How can we calculate these derivatives? ALGLIB users have several options:

1. gradient is calculated by user, usually through symbolic differentiation (so called analytical or exact gradient). This option is the best one because of two reasons. First, precision of such gradient is close to the machine ε (that's why it is called exact gradient). Second, computational complexity of N-component gradient is often only several times (not N times!) higher than calculation of function itself (knowledge of the function's structure allows us to calculate gradient in parallel with function calculation).
2. gradient is calculated by ALGLIB through numerical differentiation, using 4-point difference formula. In this case user calculates function value only, leaving all differentiation-related questions to ALGLIB package. This option is more convenient than previous one because user don't have to write code which calculates derivative. It allows fast and easy prototyping. However, we can note two significant drawbacks. First, numerical gradient is inherently inexact (even with 4-point differentiation formula), which can slow down algorithm convergence. Second, numerical differentiation needs 4·N function evaluations in order to get just one gradient value. Thus numerical differentiation will be efficient for small-dimensional (tens of variables) problems only. On medium or large-scale problems algorithm will work, but very, very slow.
3. gradient is calculated by user through automatic differentiation. As result, optimizer will get cheap and exact analytical gradient, and user will be freed from necessity to manually differentiate function. ALGLIB package does not support automatic differentiation (AD), but we can recommend several AD packages which can be used to calculate gradient and pass it to ALGLIB optimizers:
   • AutoDiff for C#
   • FuncDesigner for Python
   • FADBAD++ for C++

Depending on the specific option chosen by you, you will use different functions to create optimizer and start optimization. If you want to optimize with user-supplied gradient (either manually calculated or obtained through automatic differentiation), then you should:

• create optimizer with minbleiccreate function
• pass callback calculating function value and gradient (simultaneously) to minbleicoptimize. If you erroneously pass callback calculating function value only then optimizer will generate exception on the first attempt to use gradient.

If you want to use ALGLIB-supplied numerical differentiation, then you should:

• create optimizer with minbleiccreatef function. This function accepts one additional parameter - differentiation step. Numerical differentiation is done with fixed step. However, step size can be different for different variables (depending on their scale set by minbleicsetscale call).
• pass callback calculating function value (but not gradient) to minbleicoptimize. If you erroneously pass callback calculating gradient then optimizer will generate exception.

Scale of the variables

Before you start to use optimizer, we recommend you to set scale of the variables with minbleicsetscale function. Scaling is essential for correct work of the stopping criteria (and sometimes for convergence of optimizer). You can do without scaling if your problem is well scaled. However, if some variables are up to 100 times different in magnitude, we recommend you to tell solver about their scale. And we strongly recommend to set scaling in case of larger difference in magnitudes.

We recommend you to read separate article on variable scaling, which is worth reading unless you solve some simple toy problem.

Preconditioner

Preconditioning is a transformation which transforms optimization problem into a form more suitable to solution. Usually this transformation takes form of the linear change of the variables - multiplication by the preconditioner matrix. The most simple form of the preconditioning is a scaling of the variables (diagonal preconditioner) with carefully chosen coefficients. We recommend you to read article about preconditioning, below you can find the most important information from it.

You will need preconditioner if:

• your variables have wildly different magnitudes (thousand times and higher)
• your function rapidly changes in some directions and slowly - in other ones
• analysis of Hessian matrix suggests that your problem is ill-conditioned
• you want to accelerate optimization

Sometimes preconditioner just accelerates convergence, but in some difficult cases it is impossible to solve problem without good preconditioning.

ALGLIB package supports several preconditioners:

• default one, which does nothing (just identity transform). It can be activated by calling minbleicsetprecdefault.
• diagonal Hessian-based preconditioner. In order to use this preconditioner you have to calculate diagonal of the approximate Hessian (not necessarily exact Hessian) and call minbleicsetprecdiag function. Diagonal matrix must be positive definite - algorithm will throw an exception on matrix with zero or negative elements on the diagonal. This preconditioner can be used for convex functions, or in situations when function is possibly non-convex, but you can guarantee that approximate Hessian will be positive definite.
• diagonal scale-based preconditioner. This preconditioner can be turned on by minbleicsetprecscale function. It can be used when your variables have wildly different magnitudes, which makes it hard for optimizer to converge. In order to use this preconditioner you should set scale of the variables (see previous section).

Stopping conditions

Four types of inner stopping conditions can be used.

• gradient-based - scaled gradient norm is small enough (scaled gradient is a gradient which is componentwise multiplied by vector of the variable scales)
• stepsize-based - scaled step norm is small enough (scaled step is a step which is componentwise divided by vector of the variable scales)
• function-based - function change is small enough
• iteration-based - after specified number of iterations

You can set one or several conditions in different combinations with minbleicsetcond function. We recommend you to use first criterion - small value of gradient norm. This criterion guarantees that algorithm will stop only near the minimum, independently if how fast/slow we converge to it. Second and third criteria are less reliable because sometimes algorithm makes small steps even when far away from minimum.

Note #1
You should not expect that algorithm will be terminated by and only by stopping criterion you've specified. For example, algorithm may take step which will lead it exactly to the function minimum - and it will be terminated by first criterion (gradient norm is zero), even when you told it to "make 100 iterations no matter what".

Note #2
Some stopping criteria use variable scales, which should be set by separate function call (see previous section).

Constraints

BLEIC algorithm supports following kinds of constraints:

• boundary constraints, i.e. constraints of the form l_i ≤x_i ≤u_i 
• linear inequality constraints, i.e. constraints of the form a₀ ·x₀ +...+a_N-1 ·x_N-1 ≥b or a₀ ·x₀ +...+a_N-1 ·x_N-1 ≤b
• linear equality constraints, i.e. constraints of the form a₀ ·x₀ +...+a_N-1 ·x_N-1 =b

Boundary constraints can be set with minbleicsetbc function. These constraints are handled very efficiently - computational overhead for having N constraints is just O(N) additional operations per function evaluation. Finally, these constraints are always exactly satisfied. We won't calculate function at points outside of the interval given by [l_i ,u_i ]. Optimization result will be inside [l_i ,u_i ] or exactly at its boundary.

General linear constraints can be either equality or inequality ones. These constraints can be set with minbleicsetlc function. Linear constraints are handled less efficiently than boundary ones: they need O((N+Ki)·K) additional operations per function evaluation, where N is a number of variables, K - is a number of linear equality/inequality constraints, Ki is a number of inequality constraints. We also need O((N+Ki)·K ²) in order to reorthogonalize constraint matrix every time we activate/deactivate even one constraint. Finally, unlike boundary constraints, linear ones are not satisfied exactly - small error is possible, about N·ε in magnitude. For example, when we have x+y≤1 as constraint we can stop at the point which is slightly beyond the boundary specified by x+y=1.

Both types of constraints (boundary and linear ones) can be set independently of each other. You can set boundary only, linear only, or arbitrary combination of boundary/linear constraints.

Examples

In order to help you use BLEIC algorithm we've prepared several examples:

• minbleic_d_1 - this example demonstrates optimization with boundary constraints
• minbleic_d_2 - this example demonstrates optimization with general linear constraints
• minbleic_ftrim - this example shows how to minimize function with singularities at the domain boundaries. This example is discussed in more details in another article.
• minbleic_numdiff - this example shows how to minimize function using numerical differentiation.

We also recommend you to read 'Optimization tips and tricks' article, which discusses typical problems arising during optimization.

This article is intended for personal use only.

Download ALGLIB