Estimate of the condition number

The condition number of square matrix A is defined as follows:

k(A) = ||A||·||A^-1||

The condition number has the following meaning: if the machine precision equals ε, when solving a system of linear equations AX = b the order of relative error will be ε·k(A). Although the matrix condition number depends on the selected norm, if the matrix is well-conditioned, the condition number will be small in all norms, and if the matrix is ill-conditioned, the condition number will be large in all norms. Thus, the most convenient norm is usually selected. 1-norm, 2-norm and ∞-norm are used most frequently. They are as follows:

    Algorithm description
    Subroutines
    Example
    Manual entries

Algorithm description

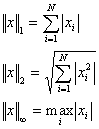
If A is given directly (i.e. we have matrix itself, not its triangular factorization), then algorithm has the following form:

1-norm of A (or ∞-norm) is calculated using closed form expression with O(N²) complexity
A is factorized using one of the triangular factorizations, O(N³) complexity
norm of A^-1 is estimated using iterative algorithm with O(N²) complexity
k(A)=norm(A)·norm(inv(A)). Overall complexity: O(N³)

If A is given by its truangular factorization (LU decomposition or Cholesky decomposition), we don't need to perform step (2). However, when performing step (1), we can't use closed form expression for matrix norm because it needs A itself, not its factorization. So following algorithm is used:

norm of A is estimated using iterative algorithm with O(N²) complexity
norm of A^-1 is estimated using iterative algorithm with O(N²) complexity
k(A)=norm(A)·norm(inv(A)). Overall complexity: O(N²)

A disadvantage of the iterative algorithm lies in the fact that it only obtains an estimate of the condition number, and a rather rough lower bound for that. An estimate is usually undersized by 5-10%, but sometimes the error is much bigger (during the numerical experiments, the estimate was lower than the condition number by 8% on average, and the maximum error was 87%). When the estimate is 10 times lower than a value itself, it is usually considered as an inaccurate estimate. Nevertheless, even such a precision may be sufficient.

Let's consider an example. Let the condition number of matrix A be equal to 10⁴. This means that if the machine precision is 10^-15, the system of linear equations will be solved with precision 10^-11. Suppose that our estimate can vary by 90% and equals 10³. This means that we can expect a higher precision: 10^-12. The difference is not very big because it is not the value of error that's important but its order. On average, 10% of the difference could be ignored since it is less than one decimal digit.

Subroutines

ALGLIB package contains a number of subroutines for condition number estimation:

RMatrixRCond1
RMatrixRCondInf
CMatrixRCond1
CMatrixRCondInf
SPDMatrixRCond
HPDMatrixRCond
RMatrixLURCond1
RMatrixLURCondInf
CMatrixLURCond1
CMatrixLURCondInf
SPDMatrixCholeskyRCond
HPDMatrixCholeskyRCond

Subroutine name depends on problem it solves and has the following form: MatrixTypeMatrix[DecompositionType]RCond[NormType].

MatrixType determines type of matrix being processed and may be R (general real), C (general complex), SPD (real symmetric positive definite) or HPD (complex Hermitian positive definite)
if subroutine accepts matrix itself, then DecompositionType is omitted. But if subroutine accepts triangular factorization of A, then factorization name as added to subroutine name (LU for general real/complex matrices, Cholesky - for SPD/HPD matrices)
subroutine name ends with description of norm used to estimate condition number: 1 - for 1-norm, Inf - for ∞-norm. However, these norms are equal for SPD/HPD matrices, so SPD/HPD subroutines have no norm suffix in their names.

Example

Let's compare condition numbers of two matrices related to the polynomial interpolation: Vandermonde matrix and matrix of Chebyshev basis functions. We'll use equidistant grid on (-1,+1). For different N's we have:

                 CONDITION NUMBERS
OF VANDERMONDE AND CHEBYSHEV INTERPOLATION MATRICES

    VANDERMONDE   CHEBYSHEV
  N      1-norm      1-norm
  2         2,0         2,0
  3         3,7         3,0
  4        18,0         4,0
  5        50,0         5,0
  6       159,4         6,0
  7       455,0         7,0
  8      1460,5         8,0
  9      4250,0         9,0
 10     13625,2        10,0
 11     40145,3        11,0
 12    128360,3        12,2
 13    381433,0        22,6
 14   1216286,9       122,8

You may see that condition number of Vandermonde matrix grows very fast, but condition number of Chebyshev matrix grows significantly slower.