LU decomposition

LU decomposition of rectangular matrix A factors matrix as product A=P·L·U of permutation matrix P (essential for the numerical stability of the algorithm), lower triangular matrix L and upper triangular matrix U. Although defined for matrices of any (rectangular) shape, it is most often applied to square NxN matrices in order to solve linear system A·x=b. Traditionally either L or U is normalized to have unit diagonal; ALGLIB convention is to normalize L.

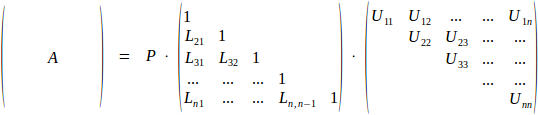
ALGLIB package has routines for LU decomposition of real and complex matrices. All versions of ALGLIB (C++, C# or other versions) provide same set of decomposition functions with similar interface.

LU decomposition functions

Storage format

One nice property of LU decomposition is that it can be stored completely in-place (well, almost completely - we still need O(N) storage for pivots). Indeed, matrix L is zero anywhere above main diagonal (and has unit diagonal, accourding to our normalization scheme), so only subdiagonal elements have to be stored. Similarly, U is zero anywhere below main diagonal, so only diagonal itself and superdiagonal elements have to be stored.

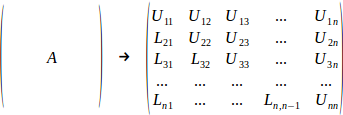
In one of subsequent sections we will show you that it is also possible to perform decomposition almost in-place, with just O(N) temporary space being allocated.

ALGLIB functions

LU decomposition is calculated by rmatrixlu (real version) and cmatrixlu (complex version) functions. Permutation matrix P is stored in separate array, L and U replace input matrix A.

Benchmarks

Comparison with other free C# libraries

In this section we compare performance of the following free C# libraries:

• ALGLIB 3.12.0 for C# (Free edition) - pure C# version of our product
• Math.NET Numerics 3.20.0 (C# backend) - well known free numerical library, compiled with C# implementation of linear algebra backend
• Accord 3.8.0 - another free numerical library written completely in C#

Although both ALGLIB for C# and Math.NET have high-performance native linear algebra kernels, for the purposes of this benchmark we evaluate performance of pure C# implementations. First, it is interesting to know how much performance NET can bring us. Second, in some cases you have to use 100% managed implementation. So, performance of NET implementation is important factor.

Our first comparison involves single-threaded LU decomposition of 1024x1024 general real matrix. This test was performed on 2.3GHz x64 Intel CPU, running Windows operating system. ALGLIB was compiled with Microsoft C# compiler, for other products we used precompiled NET 4.5 assemblies.

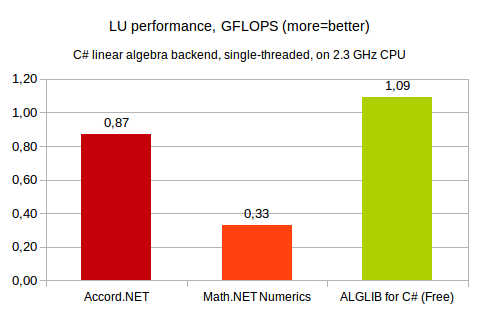
You may see that ALGLIB is the winner. Its closest competitor Accord.NET is ~20% slower, whilst Math.NET is ~3x slower than ALGLIB.

Comparing C#, C++ and SIMD implementations

ALGLIB provides several different implementations of linear algebra functionality, all with 100% identical APIs:

• 100% managed C# implementation - used by ALGLIB for C#
• generic C/C++ implementation - which can be used on platforms without high-performance SIMD-capable kernels (say, embedded systems)
• HPC implementation - highly optimized version of the library which can be used from C++ and C#, with assembly kernels for performance-intensive parts (including vendor implementations like Intel MKL)

Obviously, we expect HPC implementation to have highest performance :) But what about specific numbers on speed-ups obtained by moving from managed to native, from generic C to SIMD code? Our first comparison involves single-threaded LU decomposition of 2048x2048 real matrix. This test was performed on 2.3GHz x64 Intel CPU, running Windows operating system.

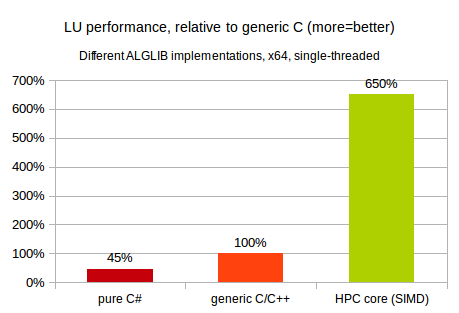
You may see that on x64 platform performance of pure C# code is ~2x times lower than that of generic C/C++ code. We optimized C# implementation of LU decomposition as much as possible, but still it is slower than generic C/C++ code without even beginner-level SIMD optimization. And, in turn, generic C/C++ code is many times slower than SIMD-capable code utilizing Intel MKL.

Implementation details

Block-matrix factorization

Naive implementation of LU decomposition scales badly with problem size - as soon as matrix size is above 64x64, it does not fit into typical L1 CPU cache, and algorithm spends most of its running time waiting for data to arrive from L2/L3 caches or RAM.

The better solution is to use block-matrix approach, which splits large matrix into smaller blocks and performs factorization step-by-step. For the sake of simplicity we consider case when no pivoting (row permutation) is performed. Algorithm below is only slightly modified when pivoting is present.

The first step is to split leading NxK submatrix from NxN input. K is typically chosen to be small, with K=32 being used quite often:

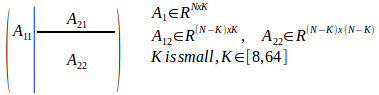
Next step involves LU factorization of much smaller NxK submatrix, with the rest of the input being unmodified for a while:

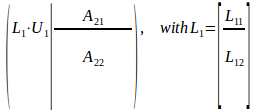
Our next step is to update the rest of the matrix with results from initial LU. Upper block A₂₁ is multiplied by inv(L₁₁), and trailing (N-K)x(N-K) matrix A₂₂ receives a bit more complex update:

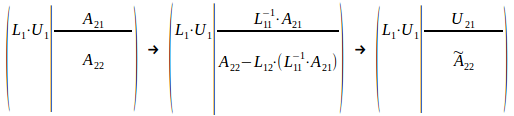
As result, we have leading K columns of L factor in L₁, leading K rows of U factor in U₁ and U₂₁ matrices, and the rest of to-be-processed A is stored in trailing N-K rows/columns. Now the only thing left is to apply same algorithm to trailing rows/columns of A, until we end up with full matrix being factorized.

One important property of such apporach is that it allows us to perform updates with highly optimized GEMM (matrix-matrix multiplication) kernels as backend. It also has potential for parallelism, because updates with large N and K can be efficiently divided between different cores.

This article is licensed for personal use only.