Student's t-tests

One of the most frequent statistical problems is testing hypotheses about the mean of the samples considered.

One-sample t-test

This test is used to check hypotheses about the fact that the mean of random variable X equals to given μ. Testing sample should be a sample of a normal random variable. During its work, the test calculates t-statistic:

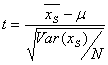
If X has a normal distribution, the t-statistic will have Student's distribution with N-1 degrees of freedom. This allows the use of the Student's distribution to define the significance level which corresponds to the value of t-statistic.

Note #1
If X is not normal, t will have an unknown distribution and, strictly speaking, the t-test is inapplicable. However, according to the central limit theorem, as the sample size increases, the distribution of t tends to be normal. Therefore, if the sample size is big, we can use the t-test even if X is not normal. But there is no way to find out what value is big enough. This value depends on how X deviates from the normal distribution. Some sources claim that N should be greater than 30, but sometimes even this size is not enough. Alternatively, we can use non-parametric test: sign test or Wilcoxon rank-sign test.

Subroutine StudentTTest1 returns three p-values:

• p-value for two-tailed test (null hypothesis - mean is equal to the given number)
• p-value for left-tailed test (null hypothesis - mean is greater than or equal to the given number)
• p-value for right-tailed test (null hypothesis - mean is less than or equal to the given number)

Two-sample pooled test

This test checks hypotheses about the fact that the means of two random variables X and Y which are represented by samples x_S and y_S are equal. The test works correctly under the following conditions:

• both random variables have a normal distribution
• dispersions are equal (or slightly different)
• samples are independent.

During its work, the test calculates t-statistic:

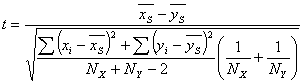
If X and Y have a normal distribution, the t-statistic will have Student's distribution with N_X+N_Y-2 degrees of freedom. This allows the use of the Student's distribution to define a significance level which corresponds to the value of t-statistic.

Note #2
If X or Y is not normal, t will have an unknown distribution and, strictly speaking, the t-test is inapplicable. However, according to the central limit theorem, as the sample sizes increase, the distribution of t tends to be normal. Therefore, if sample sizes are big enough, we can use the t-test even if X or Y is not normal. But there is no way to find what values for N_X and N_Y are big enough. These values depend on how X and Y deviate from the normal distribution. Some sources claim that N_X+N_Y should be greater than 40, but sometimes even these sizes are not enough. If you are not confident that distributions are normal, it's better to use non-parametric test: Mann-Whitney U-test.

Subroutine StudentTTest2 returns three p-values:

• p-value for two-tailed test (null hypothesis - means are equal)
• p-value for left-tailed test (null hypothesis - mean of the first sample is greater than or equal to the mean of the second sample)
• p-value for right-tailed test (null hypothesis - mean of the first sample is less than or equal to the mean of the second sample)

Two-sample unpooled test

This test checks hypotheses about the fact that the means of two random variables X and Y which are represented by samples x_S and y_S are equal. The test works correctly under the following conditions:

• both random variables have a normal distribution
• samples are independent.

Dispersion equality is not required.

During its work, the test calculates the t-statistic:

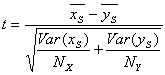
If X and Y have a normal distribution, the t-statistic will have Student's distribution with DF degrees of freedom:

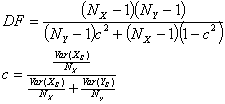
This allows the use of the Student's distribution to define the significance level which corresponds to the value of the t-statistic.

Note #3
If X or Y is not normal, t will have an unknown distribution and, strictly speaking, the t-test is inapplicable. However, according to the central limit theorem, as the sample sizes increase, the distribution of t tends to be normal. Therefore, if sample sizes are big enough, we can use the t-test even if X or Y is not normal. But there is no way to find what values for N_X and N_Y are big enough. These values depend on how X and Y deviate from the normal distribution. Some sources claim that N_X +N_Y should be greater than 40, but sometimes even these sizes are not enough. If you are not confident that the distributions are normal, it's better to use non-parametric test: Mann-Whitney U-test.

Subroutine UnequalVarianceTTest returns three p-values:

• p-value for two-tailed test (null hypothesis - means are equal)
• p-value for left-tailed test (null hypothesis - mean of the first sample is greater than or equal to the mean of the second sample)
• p-value for right-tailed test (null hypothesis - mean of the first sample is less than or equal to the mean of the second sample).

Links

1. 'Hypothesis testing', Wikipedia
2. 'P-value', Wikipedia
3. 'T-test', Wikipedia

This article is licensed for personal use only.