Principal component analysis

The Principal Component Analysis (also known as PCA) is a popular dimensionality reduction method. ALGLIB package includes highly optimized PCA implementation available in several programming languages, including:

• ALGLIB for C++, a high performance C++ library with great portability across hardware and software platforms
• ALGLIB for C#, a highly optimized C# library with two alternative backends: a pure C# implementation (100% managed code) and a high-performance native implementation (Windows, Linux) with same C# interface

Our implementation of PCA:

• supports full PCA and truncated PCA using efficient subspace eigensolver for faster extraction of low-dimension subspaces
• works with both dense and sparse datasets (sparse truncated PCA is much faster than its dense counterpart)

Getting started

PCA functionality in ALGLIB is provided by the pca subpackage of ALGLIB package. Depending on specific task being solved, you may want one of the following functions:

• pcabuildbasis, if you want to perform full-scale PCA analysis which returns complete K-dimensional basis, with variables being ordered by variance (ones capturing most of the variance come first)
• pcatruncatedsubspace, if you need just a few leading principal components (i.e. K₂≪K). Fast subspace eigensolver is used to solve low-dimensionality eigenproblem.
• pcatruncatedsubspacesparse, if your dataset is highly sparse.

These functions return orthogonal basis (either K-dimensional or truncated one).

Benchmarks

Comparing complete, truncated and sparse PCA

Complete principal component analysis algorithm performs dense singular value decomposition of the entire MxN input matrix (here M is a number of dataset records, N is a number of variables). Singular value decomposition cost is O(M·N²) which is often prohibitively large. Truncated version of the PCA algorithm uses subspace eigensolver which can extract k leading eigenvalues. Cost of one truncated PCA iteration is O(M·N·k); typically just 10 or 20 iterations are required. It is also possible to utilize sparsity of the dataset matrix.

In our first benchmark we will compare complete, dense truncated and sparse trunctated principal component analysis using dense 10000x1000 problem (10000 points, 1000 variables), with truncated PCA being configured to extract top 10 principal components. Fill factor of the sparse matrix is 1%. We used HPC edition of ALGLIB 3.14 (SIMD kernels, multithreading) running at 3.5 GHz Intel CPU for comparison.

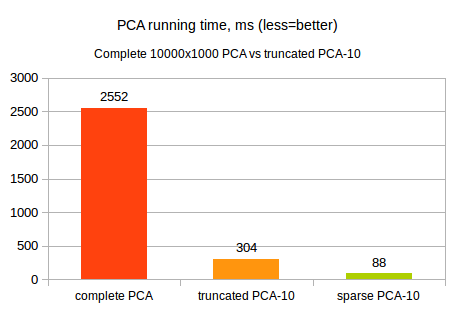
As you may see, switching to truncated version results in roughly 8x increase in performance. And sparsity support adds additional 3x multiplicative speed-up! However, we should note that specific value of the performance gain heavily depends on the problem metrics: dataset size, distribution of the eigenvalues, number of the principal components being extracted.

Comparing C#, C++ and HPC implementations

Both versions of the PCA algorithm (full and truncated) heavily depend on the underlying linear algebra code. ALGLIB has several different implementations of linear algebra functionality (and PCA), all with 100% identical APIs, but different performance:

• 100% managed C# implementation - used by ALGLIB for C# (commercial and open source editions)
• open source C/C++ implementation - which can be used on platforms without high-performance SIMD-capable kernels
• HPC implementation - highly optimized version of the library which can be used from C++ and C#, with assembly kernels for performance-intensive parts (including vendor implementations like Intel MKL)

Our comparison involves single-threaded truncated PCA of 5000x500 dataset with top 10 principal components being extracted. This test was performed ALGLIB 3.14 running on 3.5 GHz Intel CPU running Linux operating system.

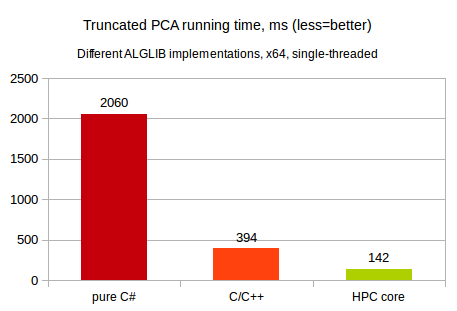
As you may see, unmanaged code is orders of magnitude faster than the managed one. And HPC edition with its SIMD kernels made by Intel is significantly faster than our open source implementation of the linear algebra.

This article is licensed for personal use only.