Multinomial logit regression

Logit regression is a linear-regression generalization for the case when the independent variable is nominal. According to the number of values taken up by the dependent variable, "just so" logit regression (two values) is distinguished from multiple logit regression (more than two values). These two types of models are combined under the general name of Logit Regression, for the purposes of this paper.

The logit model maps the vector of independent variables x in a vector of the posterior probabilities y. The mapping is specified by matrix of the coefficients A:

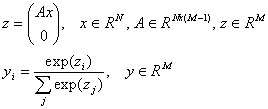
Note #1
It may be noted that the logit model is a special case of generalized linear models. On the other hand, it is a special case of a neural network, that is, a network with one linear layer and with SOFTMAX normalization.

Logit regression, similar to linear regression, is characterized by the same advantages and disadvantages: simplicity and a relatively high speed of model generation, on the one hand, but unsuitability for solving essentially nonlinear problems. When your problem is not adequately solved using logit regression, we recommend you to have a try at using one of the other algorithms of this section.

Logit regression in ALGLIB

Operations with logit models are performed in two stages:

• Model construction with the MNLTrainH subroutine. The outcome is the LogitModel structure which stores the trained model.
• Operations with the model (data processing, model copying/serialization, etc.)

Training Algorithm

The logit-model's coefficients are found by minimizing the error function on a training set. Cross-entropy (plus a regularizing term improving convergence) is used as the error function. The following algorithm is applied for minimizing: in the distance from the minimum, a step is taken in the direction of the antigradient, and an iteration is made, following the Newton method, near the minimum (using the Hessian of the error function). Before the algorithm is started, some steps are taken in the direction of the antigradient, to bring us to the neighborhood where the function's curvature is positive.

The algorithm as set forth above has both advantages and disadvantages. The main disadvantage is its complexity which is O(N·M ²·(c-1)²) per iteration using the Hessian, where N is the number of points in the training set, M is the number of independent variables, c is the number of classes. The algorithm's merits are distinctive, however: that is, the number of iterations is small (when the algorithm finds itself in the minimum vicinity, it is rapidly converging), no stopping criterion needed (algorithm always converges to exact minimum).

This article is licensed for personal use only.